Hemmes mathematische Rätsel: Das Poolbillarddreieck
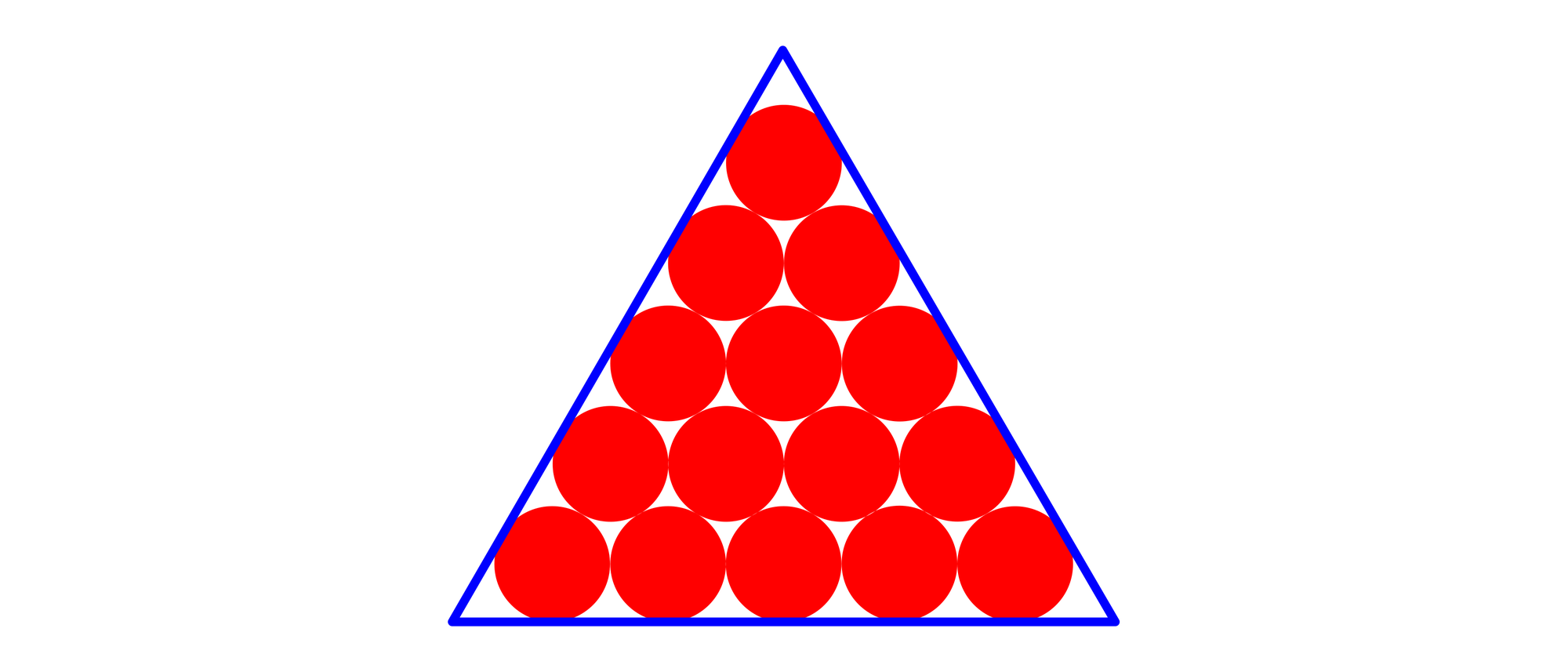
Poolbillard wird mit 15 farbigen Objektkugeln und einer weißen Spielkugel gespielt. Die Objektkugeln haben alle einen Durchmesser von 21⁄4 Zoll = 5,715 Zentimeter. Zu Beginn eines Spieles werden die 15 Objektkugeln auf dem Billardtisch zu einem dreieckigen Muster angeordnet, auf die dann der erste Spieler die weiße Kugel mit dem Queue stößt. Um das Anordnen der Kugeln zu erleichtern, legt man einen dreieckigen Holz- oder Kunststoffrahmen auf den Billardtisch, setzt die 15 Kugeln dort hinein und entfernt den Rahmen anschließend vorsichtig.
Diese Rahmen, deren Höhe einen Kugelradius übersteigt, sind meistens keine exakten Dreiecke, sondern an den Ecken etwas abgerundet. Nehmen wir aber dennoch einmal an, sie wären perfekte gleichseitige Dreiecke. Wie lang muss dann die Innenseitenlänge mindestens sein, damit alle 15 Kugeln hineinpassen?
Um das Problem zu lösen, reicht es aus, nur die halbe untere Kugelreihe und die halbe untere Dreiecksseite L/2 zu betrachten.
Sie setzt sich aus vier Kugeldurchmessern und der Strecke a zusammen und hat somit die Länge L/2 = a + 2d. Die Kugel in der Ecke des Billarddreiecks bildet mit einem ihren Radien und der Verbindungslinie von ihrem Mittelpunkt zur Ecke ein rechtwinkliges Dreieck.
Da das Billarddreieck gleichseitig ist und seine Winkel folglich alle 60° betragen, hat das rechtwinklige Dreieck dort einen Winkel von 30°. Somit gilt tan 30° = d/(2a) und a = d/(2 tan 30°) = 1⁄2d√3.
Daraus ergibt sich eine Seitenlänge des Billarddreiecks von L = (4 + √3) d ≈ 12,897 Zoll ≈ 32,758 Zentimeter.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.