Hemmes mathematische Rätsel: Das triangulierte Rechteck
Geometrische Rätsel und Probleme beschäftigen die Menschen schon seit Jahrtausenden. Man findet sie zuhauf auf Papyri aus Ägypten, auf Keilschrifttafeln aus dem Zweistromland und auf Pergamenten aus Griechenland. Und auch die Perser, Inder und Chinesen des Altertums haben sich intensiv mit ihnen auseinandergesetzt. Die Geometrie hat auch in der Gegenwart noch nicht ihren Reiz als intellektuelle Unterhaltung verloren. Das heutige Rätsel ist ein modernes geometrisches Problem.
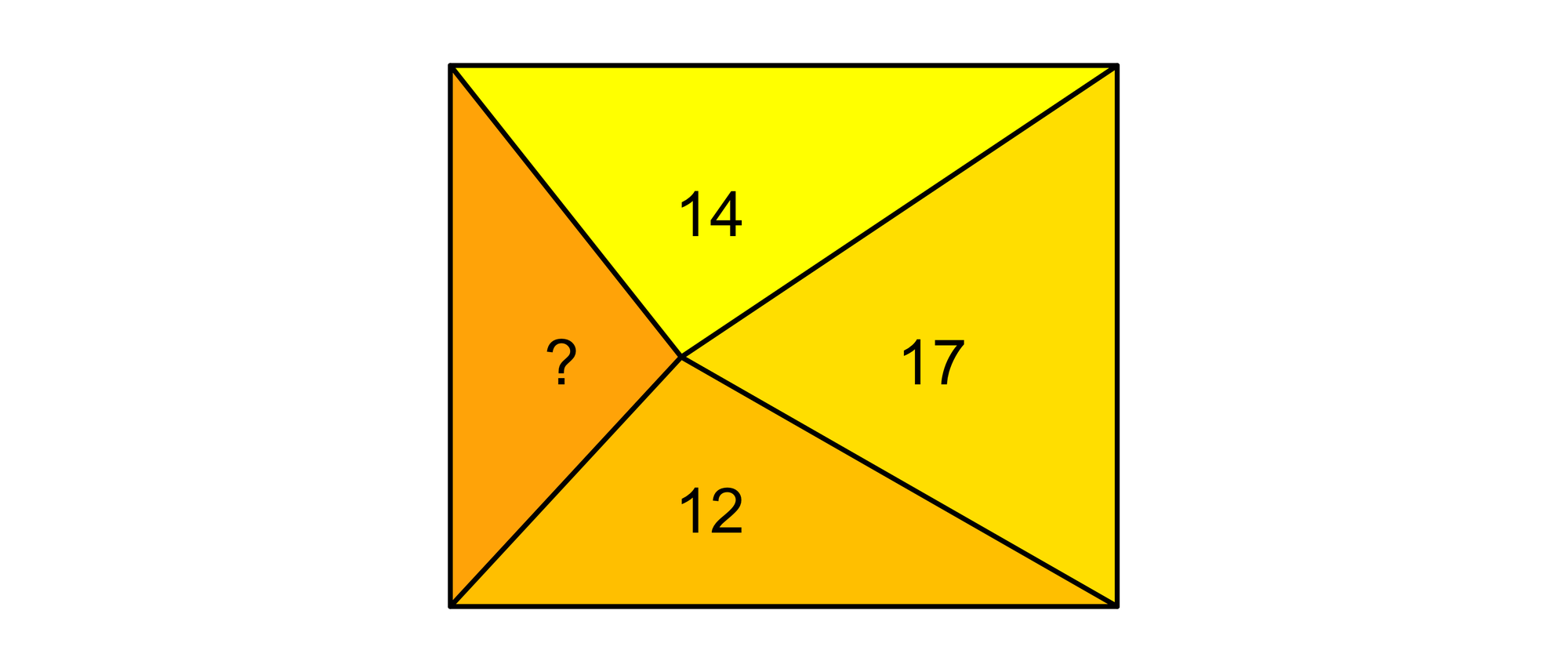
Ein Rechteck ist in vier Dreiecke unterteilt, die Zahlen geben ihre Flächeninhalte an. Bei einem Dreieck fehlt jedoch diese Zahl. Wie groß ist sein Flächeninhalt?
Zeichnet man zwei Parallelen zu den Außenlinien der Figur, die durch den gemeinsamen Punkt der vier Dreiecke verlaufen, zerfällt sie in vier Rechtecke, die durch Diagonalen halbiert sind.
Da die Summe von je einer Hälfte der beiden unteren Rechtecke 12 beträgt und die Summe von je einer Hälfte der beiden oberen Rechtecke 14, muss die gesamte Figur einen Inhalt von 2(12 + 14) = 52 haben.
Zieht man hiervon die Inhalte der drei bekannten Dreiecke ab, bleibt für das unbekannte Dreieck noch eine Fläche von 9 übrig.



Schreiben Sie uns!
Beitrag schreiben