Hemmes mathematische Rätsel: Der einsame Turm
Henry Ernest Dudeney war wohl der bedeutendste Rätselerfinder, der jemals lebte. Er wurde 1857 in Mayfield in England geboren und starb 1930. Dudeney entwarf über Jahrzehnte für zahlreiche Zeitungen regelmäßig Denksportprobleme. Die meisten seiner Rätsel fasste er später auch zu Büchern zusammen, die zum Teil heute noch erhältlich sind. Die folgende Aufgabe stammt aus seinem Werk »Amusement in Mathematics«.
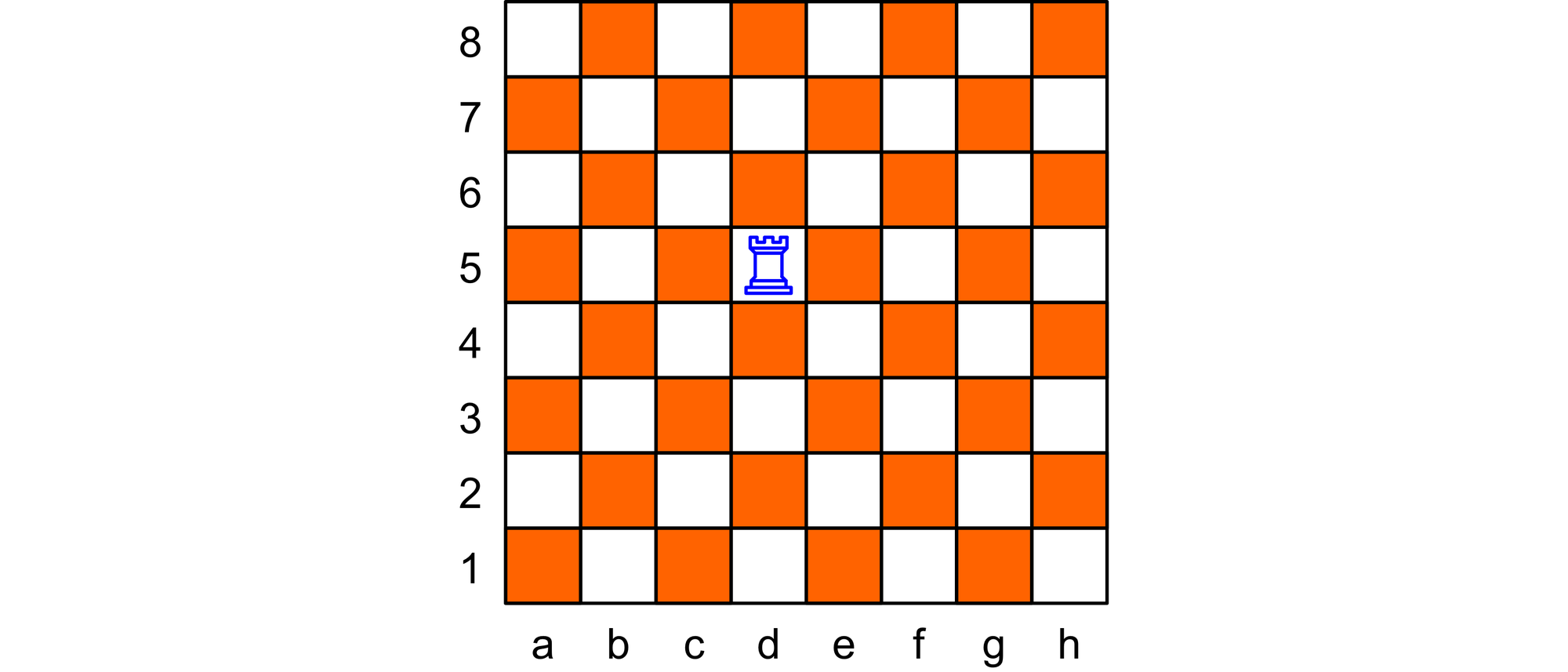
Ein Turm steht auf dem Feld d5 eines Schachbretts und soll mit möglichst wenigen Zügen einmal über alle Felder des Bretts gezogen werden und zum Schluss wieder zum Ausgangsfeld zurück gelangen.
Dabei darf der Turm kein Feld mehrmals betreten. Eine Ausnahme ist das Startfeld, das ja gleichzeitig das Zielfeld ist, und darum insgesamt zweimal betreten werden muss. Der Turm darf nur die beim Schach üblichen Züge machen. Ein Feld gilt auch dann als betreten, wenn der Turm bei einem Zug nur über dieses Feld läuft. Zieht also beispielsweise der Turm von a1 nach a4, so hat er dabei auch die Felder a2 und a3 betreten. Wie viele Züge sind mindestens für diese Rundtour notwendig?
Falls es auf dem Brett eine vertikale Felderreihe gibt, in der der Turm keinen vertikalen Zug macht, muss man alle Felder horizontal überqueren. Folglich muss es dann mindestens acht horizontale Züge geben.
Wenn man jedoch in jeder vertikalen Reihe mindestens einmal vertikal zieht, macht man einschließlich der Rückkehr zum Ausgangsfeld ebenfalls acht horizontale Züge, um von einer Reihe zur nächsten zu kommen.
Ganz analog kann man beweisen, dass es auch mindestens acht vertikale Züge geben muss. Das bedeutet, insgesamt muss der Turm mindestens 16 Züge für seine Rundtour machen.
Dass diese auch tatsächlich ausreichen, sieht man an den beiden Beispielen. Es sind übrigens die einzigen Basislösungen, die es gibt. Aus ihnen kann man durch Drehungen und Spiegelungen des Brettes noch sechs weitere ableiten.
Schreiben Sie uns!
Beitrag schreiben