Hemmes mathematische Rätsel: Der Widerstandswürfel
Im Jahre 1920 erschien die erste Auflage des Buches »Magnetism and Electricity: A Manual for Students in Advanced Classes« von Ernest Edward Brooks und Arthur William Poyser. Dieses Lehrbuch wurde zu einem Standardwerk der Elektrotechnik ist auch heute noch im Buchhandel zu kaufen. Es enthält zahlreichen Übungsaufgaben, darunter auch das Problem des Widerstandswürfels, das sich seitdem zu einem Denksportklassiker entwickelt hat.
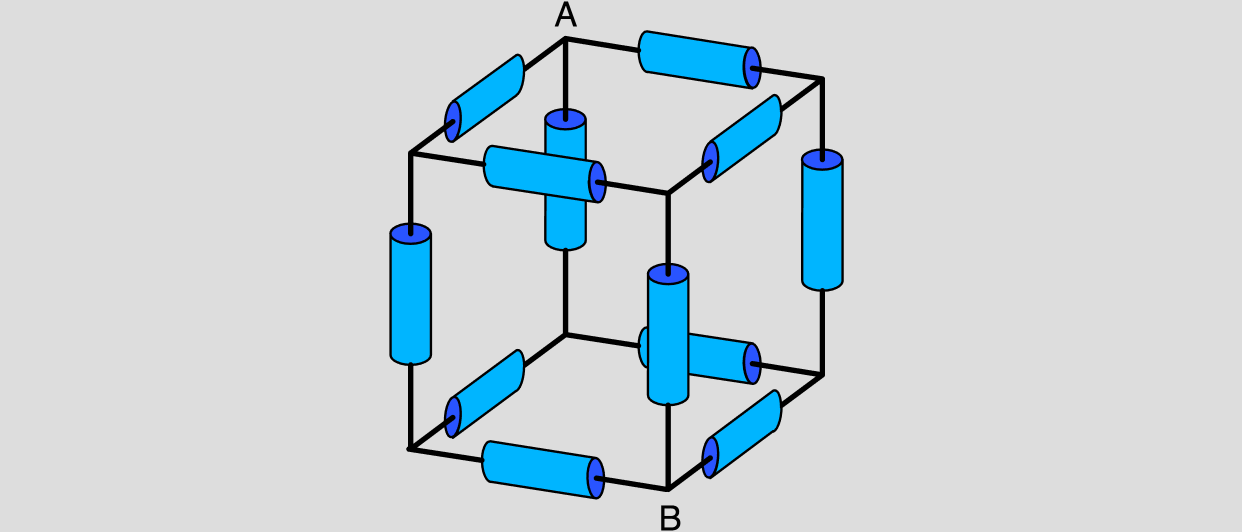
Das Skelett eines Würfels, das von seinen Kanten und Ecken gebildet wird, ist aus zwölf 1-Ohm-Widerständen zusammengelötet worden. Wie groß ist der Gesamtwiderstand zwischen den beiden sich diagonal gegenüberliegenden Ecken A und B?
Erinnerung: Werden n Widerstände R1, R2, R3, …, Rn in Reihe geschaltet, ist der Gesamtwiderstand R die Summe R = R1 + R2 + R3 + … + Rn der Einzelwiderstande. Werden hingegen n Widerstände parallel geschaltet, ist der Gesamtwiderstand R nicht die Summe der n Widerstände, sondern die Summe der Kehrwerte der Widerstände ist der Kehrwert des Gesamtwiderstands: 1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn.
Damit der Widerstandswürfel etwas anschaulicher wird, verzerren wir ihn soweit, bis er sich in der Ebene flach ausbreiten lässt, ohne dass es zu Überschneidungen der Widerstände kommt. Den Punkt B ziehen wir dabei zu einem Kreis auseinander.
Die drei Würfelecken U, V und W liegen aus Symmetriegründen auf dem gleichen elektrischen Potential, darum darf man sie getrost miteinander verbinden, ohne dass sich der Widerstand des Systems ändert. Das gleiche gilt für die Ecken X, Y und Z. Jetzt sieht man, dass die Widerstände zwischen den einzelnen Kreisen parallel und die Kreise selbst hintereinander geschaltet sind.
Daraus ergibt sich der Gesamtwiderstand 1/3 Ohm + 1/6 Ohm + 1/3 Ohm = 5/6 Ohm.



Schreiben Sie uns!
Beitrag schreiben