Hemmes mathematische Rätsel: Die Dreiteilung der Fläche
Nobuyuki Yoshigahara war Japans bedeutendster Puzzle- und Rätselerfinder. Er wurde am 27. Mai 1936 geboren und arbeitete zunächst als Chemiker und später, nach einem Laborunfall, als Chemie- und Mathematiklehrer. Er verfasste mehr als 70 Bücher über Denksportaufgaben und schrieb zahlreiche Rätselkolumnen, zeitweilig waren es siebzehn pro Monat. Yoshigahara ist der Erfinder zahlloser mechanischer Puzzles, von denen viele auch von Spielzeugherstellern produziert und vertrieben werden. Er war einer der Begründer der »International Puzzle Party«, bei der sich einmal jährlich die Puzzleexperten der Welt treffen. Yoshigahara starb am 19. Juni 2004. 2005 wurde der von ihm 2001 ins Leben gerufene Puzzleentwurfswettbewerb ihm zu Ehren in »Nob Yoshigahara Puzzle Design Competition« umbenannt. In dem von Elwyn Berlekamp und Tom Rodgers herausgegebenen Buch »The Mathemagician and Pied Puzzler«, das 1999 in den USA erschien, stellte Yoshigahara den Lesern das folgende Teilungsproblem:
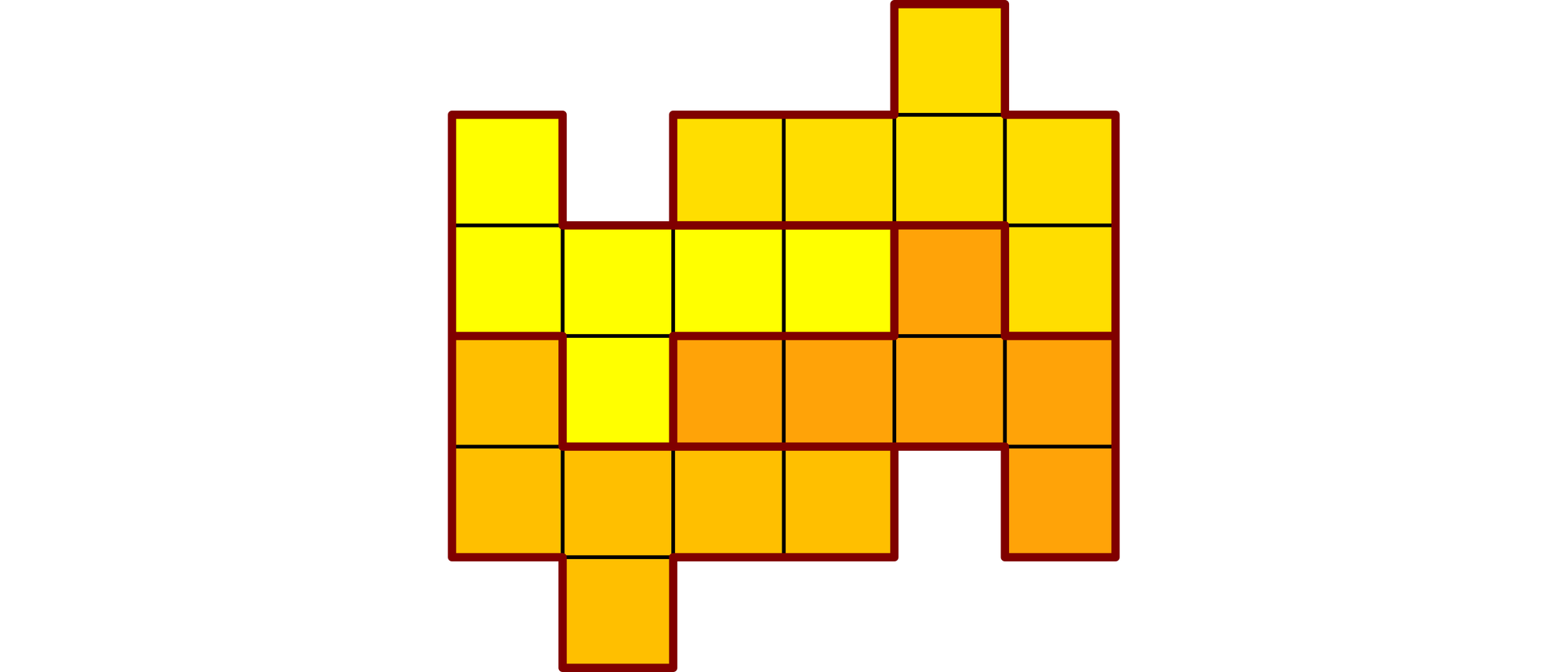
Die 20-eckige Figur aus der Skizze besteht aus 24 kleinen Quadraten. Sie ist in vier deckungsgleiche Flächen unterteilt. Kann man die Figur auch in drei deckungsgleiche Stücke zerlegen?
Nobuyuki Yoshigahara hat in sein Rätsel eine kleine Denkschwelle eingebaut: Man nimmt unwillkürlich an, dass die Schnitte nur entlang der Quadratgrenzen erfolgen dürfen, obwohl er das mit keiner Silbe verlangt hat. Das quadratische Raster dient also nur zur Verwirrung. Hat man diese Schwelle erst einmal überstiegen, ist die Aufgabe ganz einfach.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.