Die vermutlich kreativsten Erfinder von Denksportaufgaben der letzten zwei Jahrzehnte sind Serhiy Grabarchuk und seine beiden Söhne Peter und Serhiy junior. Die Familie lebt in Uzhgorod, einer kleinen Stadt im Westen der Ukraine, und hat Tausende von Knobeleien entwickelt. Die drei Rätselerfinder haben auch eine Reihe von Büchern geschrieben. In Deutsch ist davon bislang noch keines erschienen, aber auf Englisch sind im Buchhandel etwa ein Dutzend Werke erhältlich. Im Jahr 2003 erfand Serhiy Grabarchuk ein Streichholzschlangenproblem, das sofort mit großer Begeisterung von der weltweiten Gemeinde der Denksportler aufgenommen und in vielfacher Weise variiert und erweitert wurde. Die folgende Aufgabe ist Grabarchuks Originalproblem.

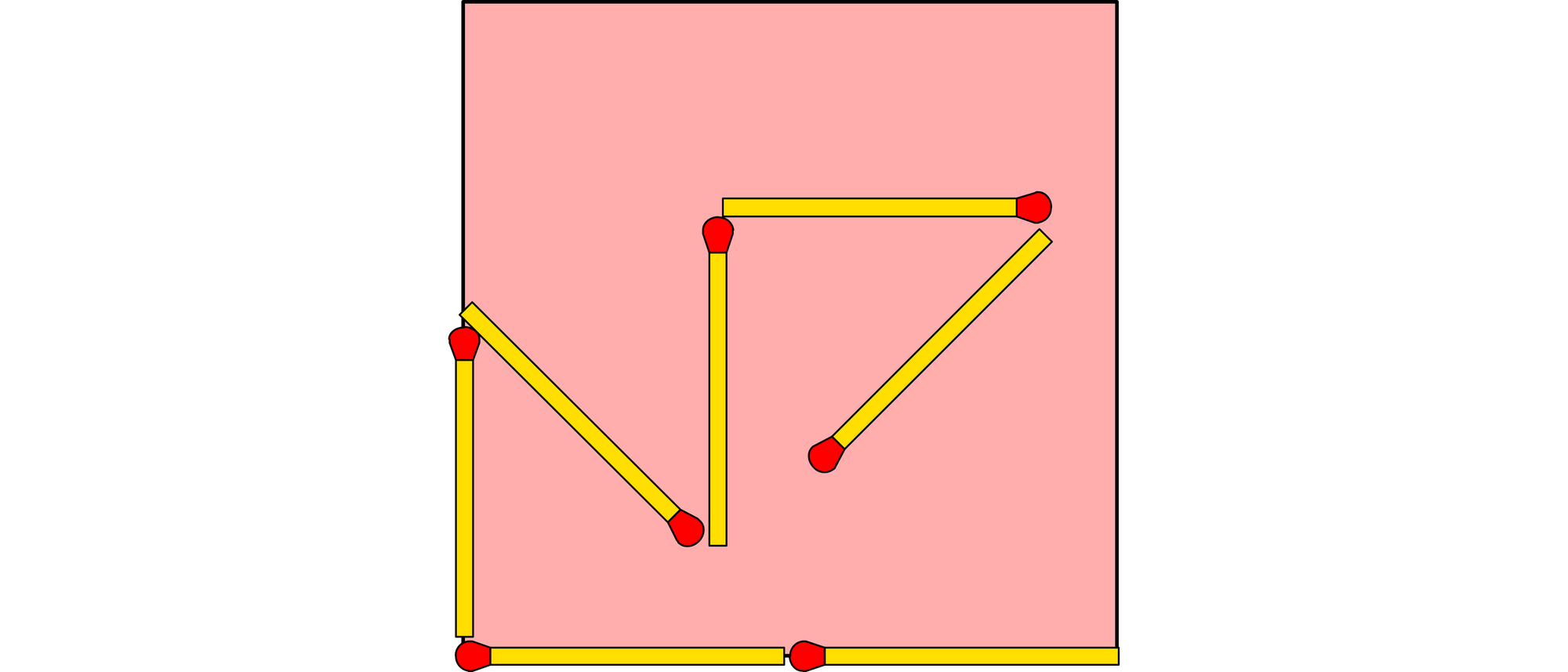
Legt man mehrere Streichhölzer so aneinander, dass der Kopf eines Holzes das Ende des nächsten Holzes berührt, entsteht eine Streichholzschlange. Legen Sie nun eine solche Streichholzschlange in ein Quadrat, dessen Seiten genau doppelt so lang sind wie ein Streichholz. Die Schlange darf sich in dem Quadrat winden, aber die Winkel zwischen benachbarten Streichhölzern dürfen nur 45 Grad, 90 Grad, 135 Grad und 180 Grad betragen. Ferner darf die Schlange sich nirgendwo selbst berühren oder überschneiden. Allerdings darf ihr Ende mit dem Anfang zusammenfallen. Einige oder alle Teile der Schlange dürfen auch auf dem Umfang des Quadrates liegen. In dem Beispiel hat die Schlange eine Länge von sieben Streichhölzern. Wie lang kann sie höchstens sein?