Hemmes mathematische Rätsel: Drei Kreise
Der 1902 in Paris geborene amerikanische Kryptograph Geoffrey Mott-Smith leitete während des Zweiten Weltkriegs beim Geheimdienst OSS die Ausbildung von Kryptographen und Kryptoanalysten. Mott-Smith war im letzten Jahrhundert auch der führende Experte für Gesellschafts- und Solitärspiele. Er schrieb alleine und zusammen mit anderen Autoren etwa 30 Bücher darüber. In den 1930er Jahren war er zudem der Herausgeber des American Contract Bridge League Bulletin. 1961 wurde ihm zu Ehren die Mott-Smith-Trophäe gestiftet, die jedes Jahr an den besten amerikanischen Bridge-Spieler vergeben wird. 1960 starb Geoffrey Mott-Smith im Alter von nur 58 Jahren. Aus seinem 1946 erschienenen Buch Mathematical Puzzles for Beginners and Enthusiasts stammt das heutige Rätsel.
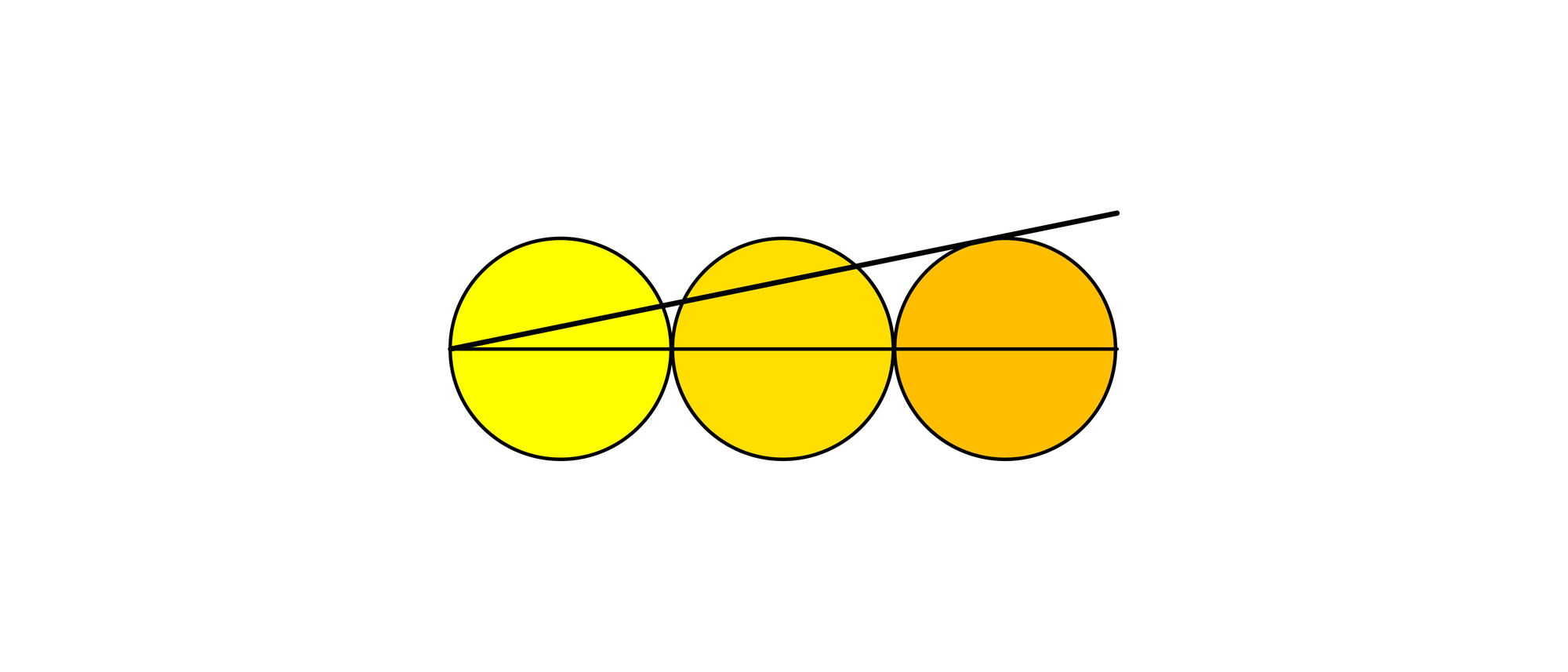
Drei Kreise von jeweils zehn Zentimeter Radius liegen direkt nebeneinander, und ihre Mittelpunkte fallen auf eine Gerade. Vom äußeren Schnittpunkt dieser Geraden mit dem Umfang des linken Kreises ist eine Tangente an den rechten Kreis gezeichnet. Wie lang ist das Stück, das der Umfang des mittleren Kreises aus der Tangente schneidet?
B und D sind die Mittelpunkte des zweiten und dritten Kreises, und die Strecke BC steht senkrecht auf der Strecke AE. Bezeichnet man den Radius der Kreise mit r, so gilt BF = DE = r, AB = 3r und AD = 5r. Da BC und DE parallel sind, folgt aus dem Strahlensatz BC⁄DE = AB⁄AD. Löst man dies nach BC auf und setzt für die Strecken die entsprechenden Vielfachen des Radius ein, erhält man BC = AB x DE ⁄ AD = 3r⁄5. Das Dreieck BCF ist rechtwinklig, deshalb gilt nach dem Satz des Pythagoras CF2 = BF2 − BC2 = r2 − (3r⁄5)2. Daraus erhält man CF = 4r⁄5. Die gesuchte Strecke GF ist doppelt so lang wie CF und hat somit die Länge 8r⁄5 = 16 cm.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.