Eins-zwei-drei im Quadrat
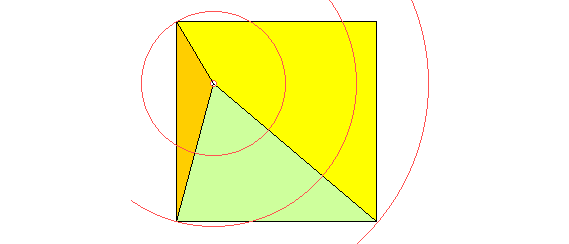
In einem Quadrat gibt es einen (hier: roten) Punkt, dessen Entfernungen sich zu drei Ecken wie 1:2:3 verhalten. Wie groß ist der stumpfe Winkel in dem orangefarbenen Dreieck?
Verdoppeln sie das Bild durch Vierteldrehung um die linke untere Ecke.
Das blaue Dreieck ist offensichtlich gleichschenklig-rechtwinklig mit Kathetenlänge 2 (Längeneinheiten); also hat das Quadrat über der Hypotenuse 8 (Flächen-)Einheiten. Damit und mit dem pythagoreischen Satz finden wir, dass auch das orangefarbdene Dreieck rechtwinklig ist. Der gesuchte Winkel beträgt somit 135o.
Wie auf Seite 163 in Honsberger "More morsels" zu lesen ist, stammen die Aufgabe aus Kvant (Problem M796) und die elegante Lösung von Murray Klamkin.
Schreiben Sie uns!
Beitrag schreiben