Erdkarte mit geraden Fluglinien
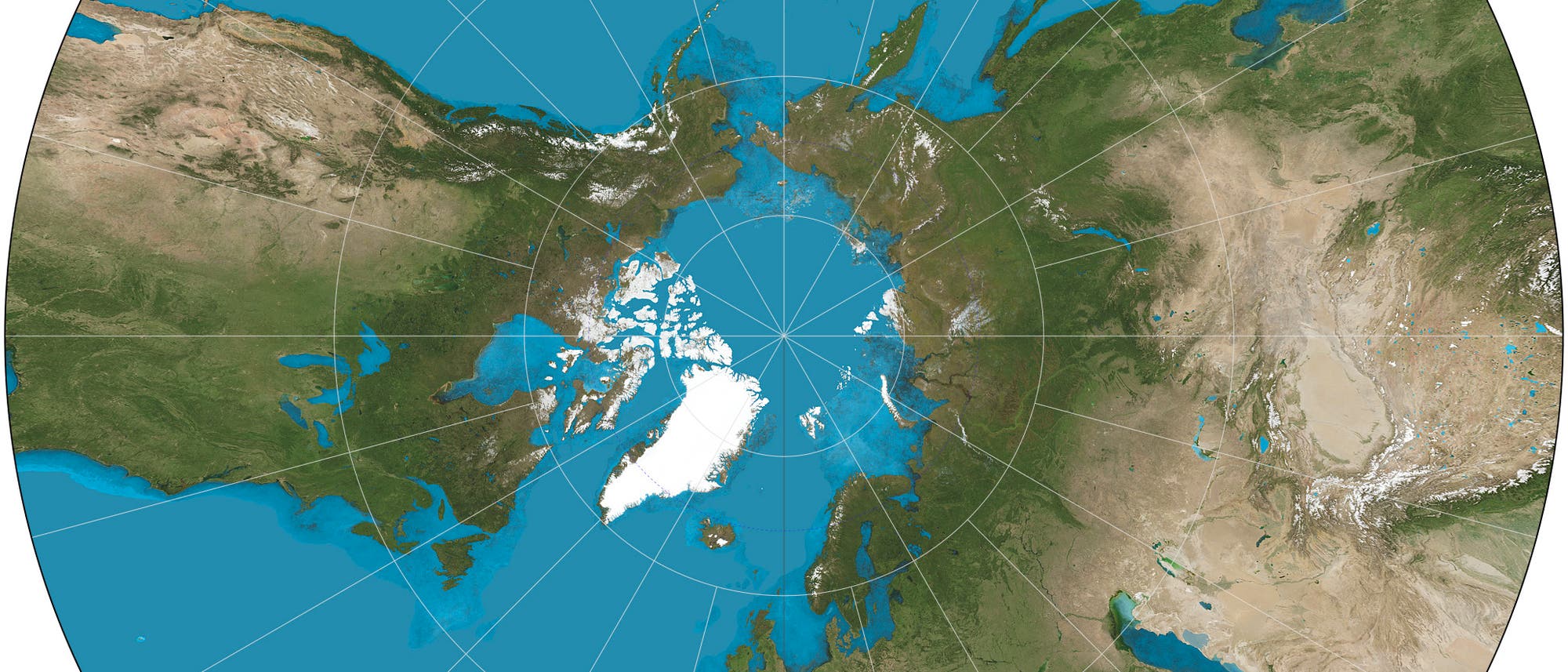
Gibt es eine ebene Erdkarte, auf der die kürzesten Verbindungen auf der Kugeloberfläche (Luftlinien) als Geraden abgebildet werden?
Zentralperspektive vom Erdmittelpunkt aus.
Wir denken uns die Erde wie einen Leuchtglobus: hohl, mit einer punktförmigen Lichtquelle im Mittelpunkt und durchscheinender Oberfläche. Irgendwo draußen halten wir eine Mattscheibe hin; was auf ihr zu sehen ist, soll unsere Erdkarte werden.
Die kürzesten Verbindungen auf der Erdoberfläche sind Teile von Kreisen um den Kugelmittelpunkt (Großkreise). Alle Punkte eines solchen bleiben bei der Zentralprojektion von der Kugelmitte aus in der Ebene ihres Kreises. Diese Ebene schneidet sich, wenn überhaupt, mit der Ebene der Mattscheibe (Kartenebene) in einer Geraden. Also muss das Bild jedes Großkreises eine gerade Linie sein.
Eine derartige Karte bildet eine halbe Kugel auf eine unendlich große Ebene ab, sie heißt "gnomonische Karte" oder "Großkreiskarte". Sie ist "echt geodätisch", das heißt, sie bildet die geodätischen Kurven (kürzesten Verbindungslinien) der Kugel (also Großkreisbögen) in solche der Ebene (also Geraden) ab.
Sie verzerrt gewaltig und ist weder flächen- noch winkeltreu. Wenn man sie aber hat und auf ihr mehrere Flughäfen, kann man diese mit dem Lineal verbinden und alle Orte ablesen, die dabei überflogen werden. Hier wird die Projektion und deren Auswirkung auf "Apfelsinenschalen" gezeigt:
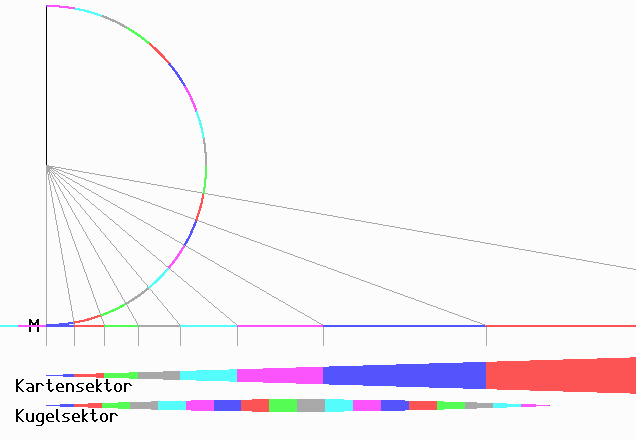

Mit dem Nordpol in der Mitte sieht die Karte so aus:
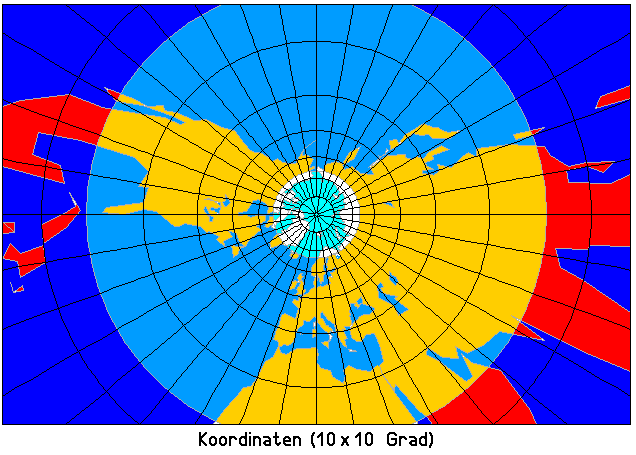
Die Speichenellipsen (Tissot-Indikatrizen, vergleiche Rätsel 604) sind stark vergrößerte Bilder von kleinen Kreisscheiben, die man sich auf dem Erdboden liegend vorstellen soll. Sie zeigen, wie Kreisscheiben (stark vergrößert dargestellt) verzerrt werden:
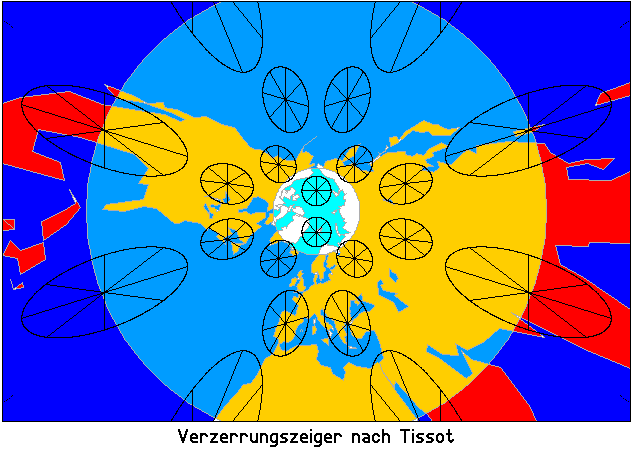
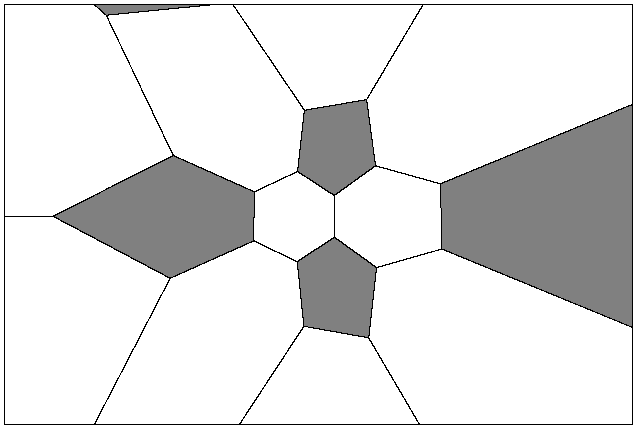
Ein Fußball (in die Kugel projizierter Ikosaederstumpf) ist dann kaum noch zu erkennen:
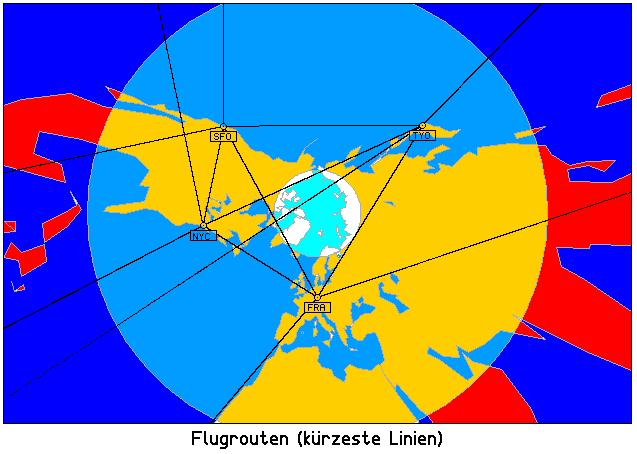
So sehen die Flugrouten (kürzeste Verbindungen auf der Erdoberfläche zwischen Start und Ziel) aus, wenn die Karte um den Nordpol konstruiert ist:
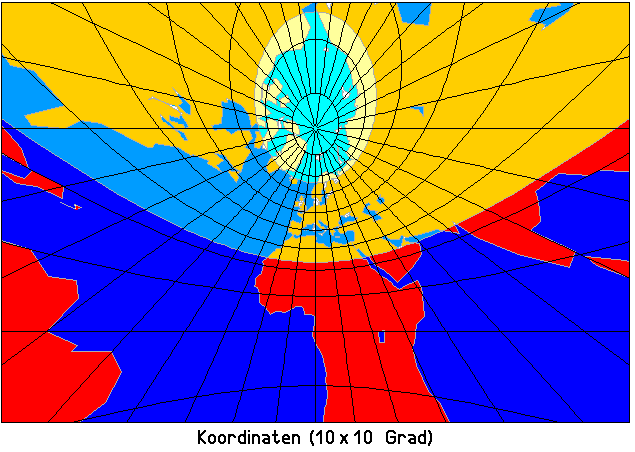
Um Mitteleuropa (Rhein-Main) herum sieht es so aus, erst mit dem Gradnetz:
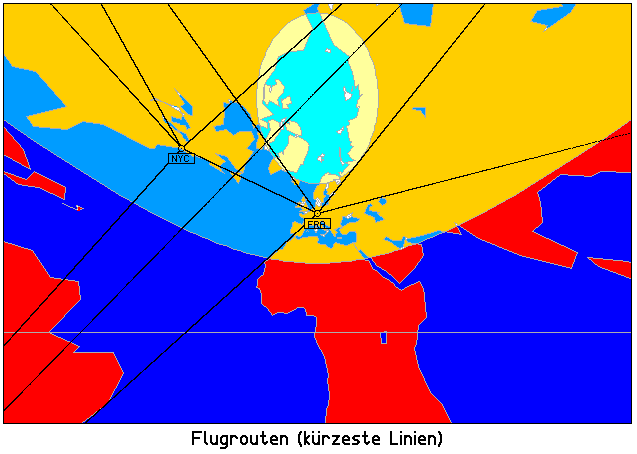
… und nun mit den Flugrouten, die wieder als Geraden erscheinen:
Dasselbe äquatorständig mit (hier aus Kegelschnitten bestehendem) Gradnetz …
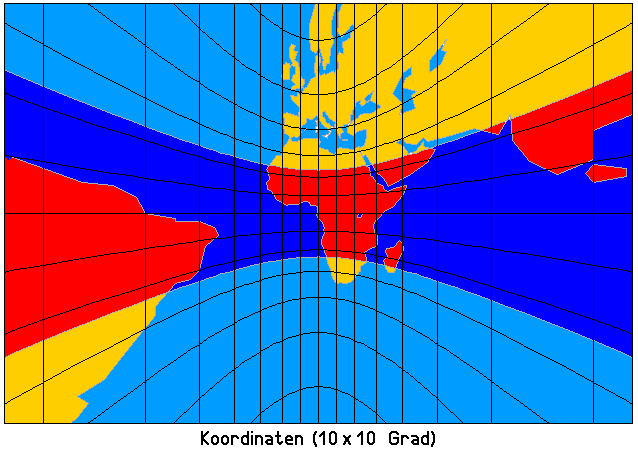
… und mit (geraden) Flugrouten:
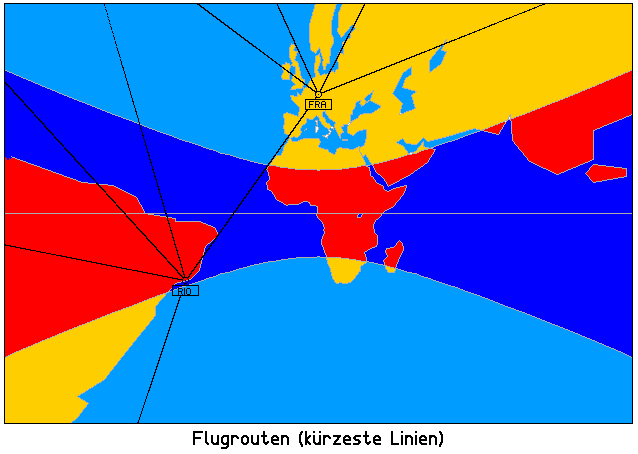



Schreiben Sie uns!
Beitrag schreiben