Lester-Kreis
June Lester hat gefunden, dass für ein nicht-gleichschenkliges Dreieck die Mittelpunkte von Umkreis und Neunpunktekreis und die beiden Fermat-Torricelli-Punkte auf einem Kreis liegen (und für das gleichschenklige natürlich auf der Symmetrieachse des Dreiecks).
Diese 4 Punkte liegen immer in der gleichen Reihenfolge auf dem Kreis, sozusagen bei der Hälfte aller (nicht-gleichschenkligen) Dreiecke im Uhrzeigersinn und bei ihren Spiegelbildern im Gegen-Uhrzeigersinn.
Man kann in einer Ebene zwei der drei Ecken eines Dreiecks festhalten und die dritte wandern lassen. Damit erhält man bis auf Drehung und Größenmaßstab alle Dreiecke.
Wo sind die Grenzlinien zwischen den beiden Sorten von nicht-gleichschenkligen Dreiecken?
Die zur Diskussion stehenden Dreiecke haben drei verschieden lange Seiten, sie unterscheiden sich von ihren jeweiligen Spiegelbildern dadurch, dass die nach fallender Länge nummerierten Seiten entweder mit oder gegen den Uhrzeiger angeordnet sind.
Wir beginnen mit dem blauen Dreieck, dessen zwei Ecken auf der waagerechten Linie fixiert sind. Die dritte Ecke ist frei beweglich.
Als Grenzen erscheinen nicht nur die waagerechte und die senkrechte Achse (was unmittelbar einleuchtet, sondern auch zwei Kreise. Wenn die dritte Ecke über sie wandert, tauschen eine größere und eine kleinere Seite ihre Rollen. Anders gesagt: Das blaue Dreieck wird gleichschenklig, wenn seine dritte Ecke auf der vertikalen Achse oder einem der beiden Kreise liegt.
Wenn die Ecke auf beiden Kreisen zugleich liegt (oben oder unten), ist das Dreieck gleichseitig, und wenn sie auf der waagerechten Achse liegt, fällt es zu einer Strecke flach.
Die verschiedenen Färbungen der Bereiche charakterisieren die Reihenfolge der vier Punkte auf dem Lester-Kreis.
Die folgenden Bilder zeigen ein Dreieck mit seinem Lester-Kreis. Hier sind zuerst einmal der Umkreis (cyan) und der Neunpunktekreis (gelb) mit ihren Mittelpunkten (Umkreis: dunkelblau und Neunpunktekreis: pink) abgebildet:
Mit außen angesetzten gleichseitigen Dreiecken (cyan) findet man den ersten Fermat-Torricelli-Punkt (grün):
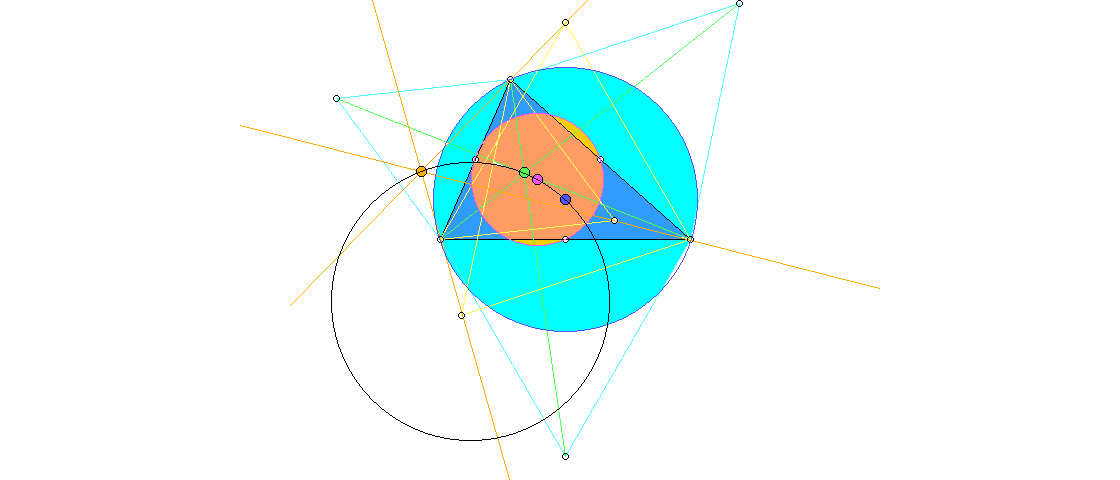
Setzt man die Dreiecke nach innen (gelb), gibt es den zweiten Fermat-Torricelli-Punkt (orange), und wir haben alle vier Punkte für den Lester-Kreis:
Bei diesem Dreieck, in dem die Seiten nach fallender Länge im Gegen-Uhrzeigersinn angeordnet sind, liegen die vier Punkte ebenfalls entgegen dem Uhrzeigersinn: Umkreismitte – Neunpunktekreis-Mitte – 1. Fermat-Torricelli-Punkt – 2. Fermat-Torricelli-Punkt.
Schreiben Sie uns!
Beitrag schreiben