Ein Satz über Höhen
© Spektrum der Wissenschaft / Manon Bischoff (Ausschnitt)
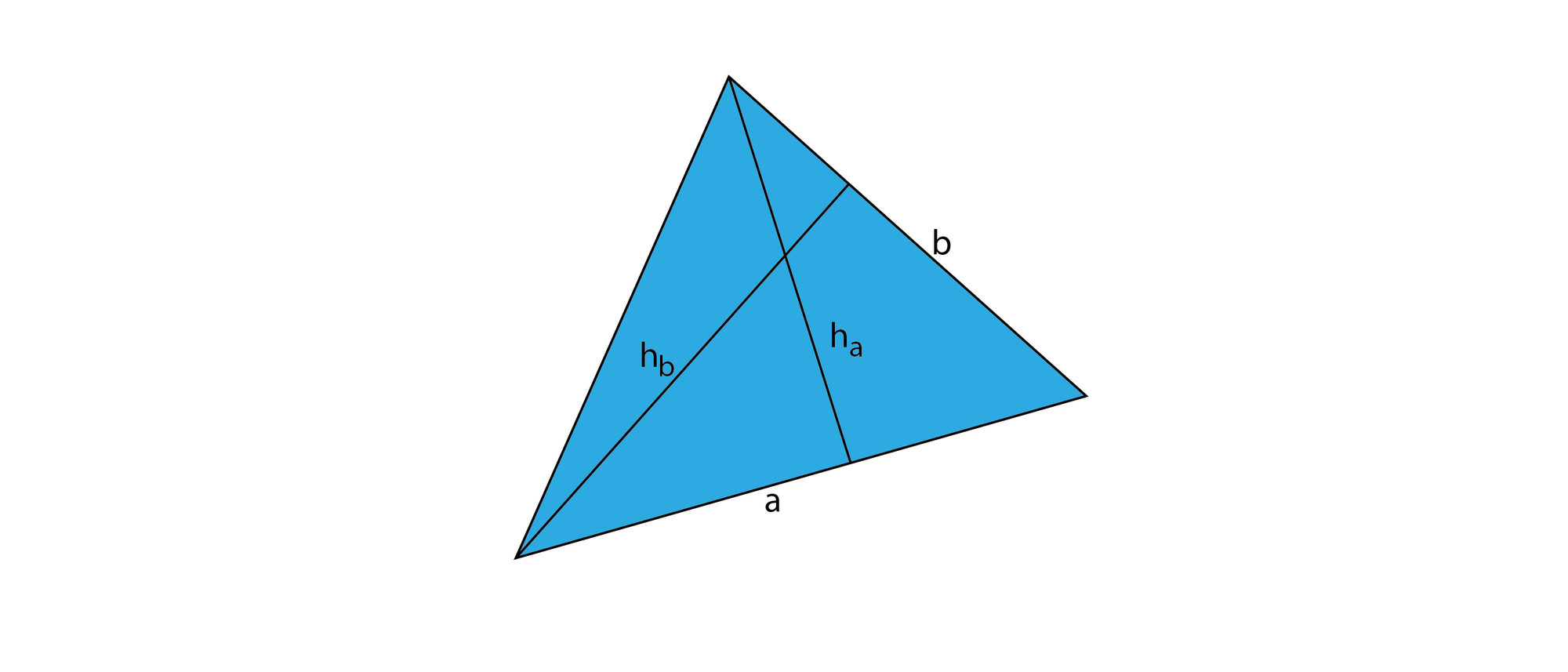
Wie kann man besonders leicht sehen, dass sich zwei Höhen in einem Dreieck umgekehrt verhalten wie die zugehörigen Seiten?
Das Produkt aus einer Seitenlänge \(l\) und der zugehörigen Höhe \(h_l\) entspricht der doppelten Fläche \(A\) des Dreiecks: nämlich der Fläche eines Parallelogramms. Daraus folgt: \(2 A = a \cdot h_a = b \cdot h_b = c \cdot h_c\).
Stellt man einen Teil dieser Formel um, erhält man: \(\frac{a}{b}=\frac{h_b}{h_a}\).
Schreiben Sie uns!
Beitrag schreiben