Hemmes mathematische Rätsel: Münzsprünge
Rodolfo Kurchan und Jaime Poniachik sind im ganzen spanischsprachigen Süd- und Mittelamerika bekannte Rätsel- und Spieleerfinder. Kurchan wurde 1971 in Buenos Aires in Argentinien und Poniachik 1943 in Montevideo in Uruguay geboren. Letzterer starb 2011 in Argentinien. 2009 schrieben sie gemeinsam das Denksportaufgabenbuch Nuevos Solitarios Clásicos, aus dem das heutige Rätsel stammt.
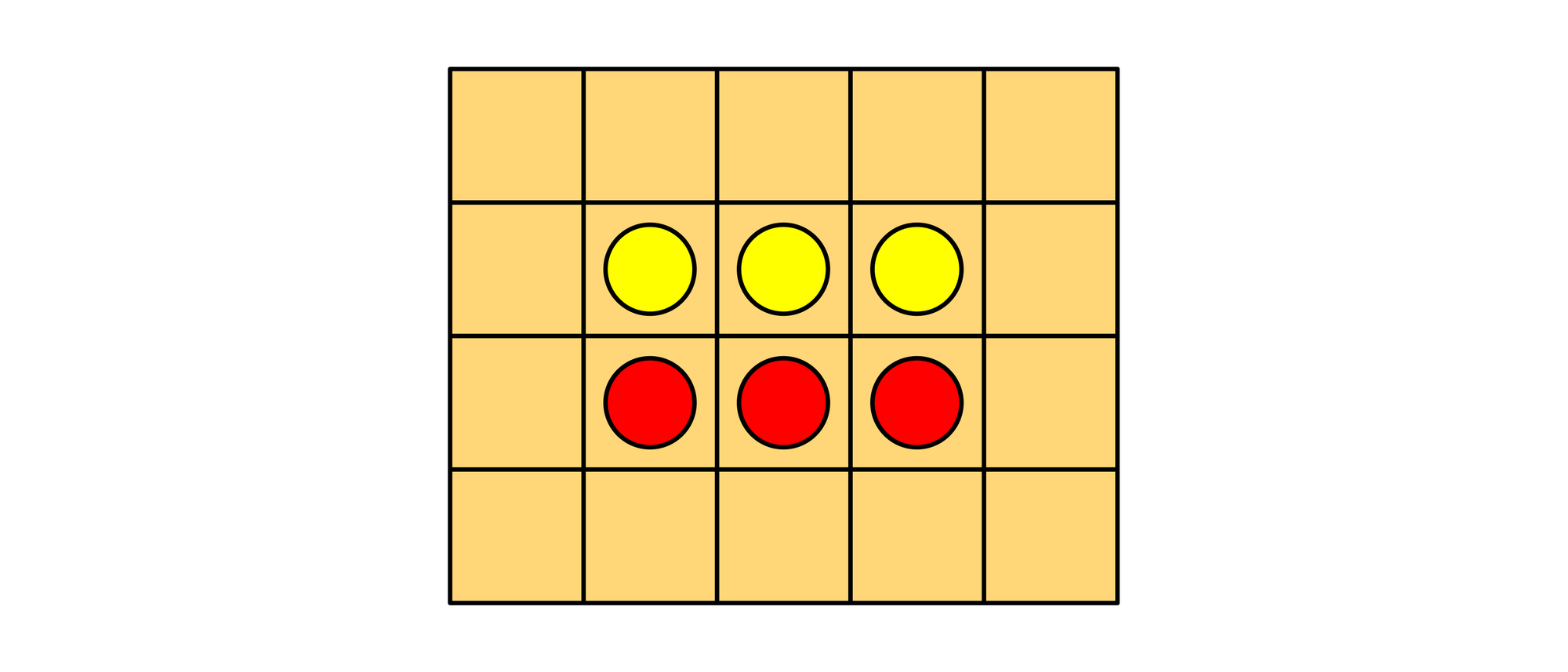
Auf einem kleinen Schachbrett mit nur 5×4 Feldern liegen sich in der Mitte eine Reihe aus drei Zehn-Cent-Münzen (gelb) und eine Reihe aus drei Fünf-Cent-Münzen (rot) gegenüber. Die Zehner und die Fünfer sollen ihre Plätze tauschen, so dass am Ende sich wieder zwei Reihen in der Mitte des Brettes gegenüberstehen, allerdings stehen dann die Fünfer oben und die Zehner unten.
Um ihre Plätze zu tauschen, dürfen die Münzen beliebig weite horizontale, vertikale und diagonale Sprünge machen. Dabei muss immer eine andere Münze oder eine Reihe lückenlos nebeneinanderliegender Münzen übersprungen werden. Ein Sprung endet immer auf dem ersten freien Feld hinter der übersprungenen Münze oder der übersprungenen Reihe. Die Skizze zeigt zwei Beispiele für erlaubte Sprünge. Führt man mit derselben Münze mehrere Sprünge in Folge aus, so wie in dem zweiten Beispiel, zählen diese nur als ein einziger Sprung.
Wie viele Sprünge müssen mindestens gemacht werden, um den Tausch zu bewältigen?
Mit dem ersten Sprung muss eine Münze, zum Beispiel ein Zehner, ein Feld im Mittelbereich des Bretts freimachen. Danach kann ein Fünfer das freigewordene Feld besetzen. Wenn nun immer abwechselnd ein Zehner und ein Fünfer springen und dabei jeweils ein Feld freimachen und das zuvor freigewordene Feld besetzen, kann zum Schluss die erste Münze mit einem letzten Sprung den Plätzetausch abschließen. Somit könnten insgesamt sieben Sprünge ausreichen. Der Wiener Mathematiker Helmut Postl probierte 2018 mit dem Computer alle Möglichkeiten durch, fand jedoch keine einzige Siebensprunglösung. Lösungen mit acht Sprüngen lassen sich aber mit etwas Mühe finden.
1. C3 → A1 2. D2 → A2 → C4 → C1 → C3 3. D3 → B1 → B4 → D2 4. B2 → D4 → D1 → D3 5. B3 → D1 → D4 → B2 6. C2 → A2 7. A1 → A3 → C1 → C4 → C2 8. A2 → E2 → C4 → C1 → E3 → B3
Schreiben Sie uns!
Beitrag schreiben