Hemmes mathematische Rätsel: Papierquadrate
Der US-Amerikaner Terry Stickels wurde 1948 in Nebraska geboren und lebt heute in Texas. Er betreibt seit vielen Jahren etliche Rätselkolumnen in Zeitungen und Magazinen und hat mehrere Dutzend Denksportaufgabenbücher geschrieben. Seit jüngstes Knobelbuch heißt »Contemporary Brainteaser« und ist 2016 erschienen. Daraus stammt das heutige Rätsel.
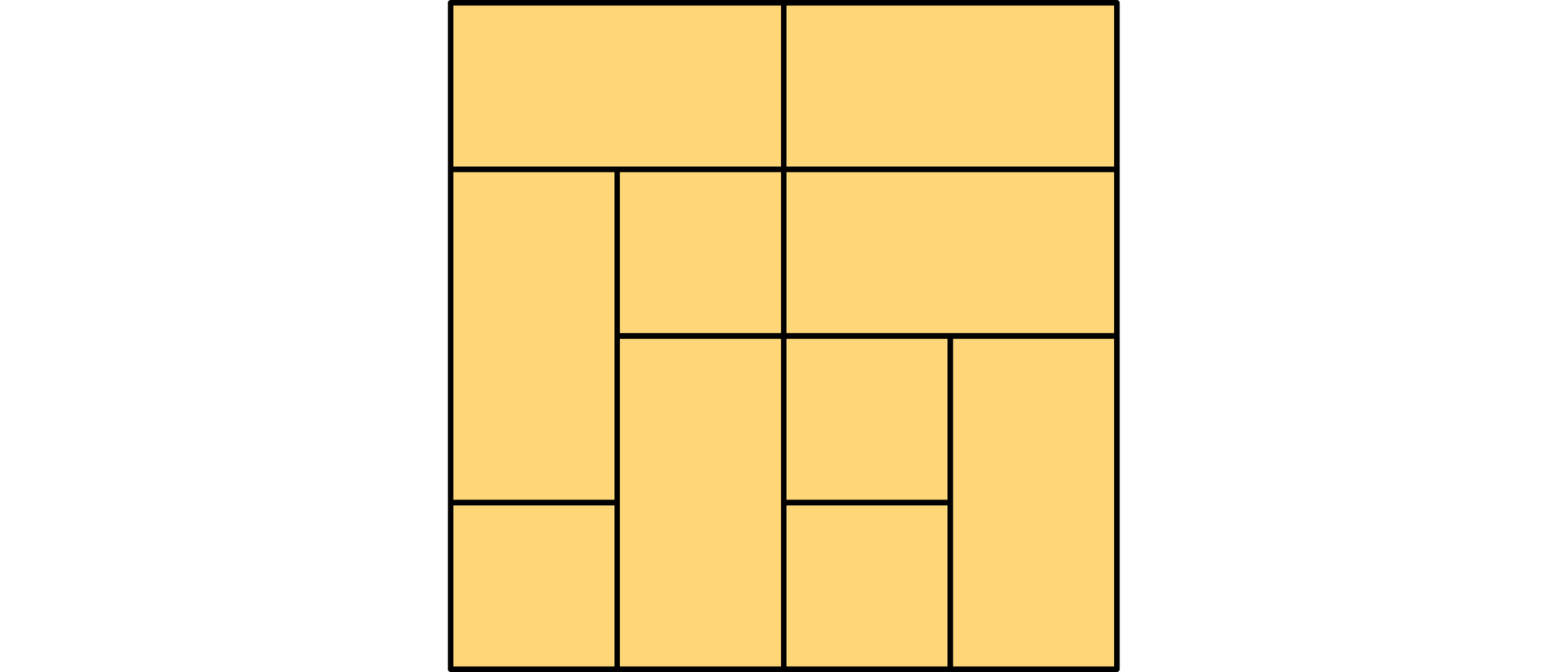
Das Muster zeigt einen Stapel quadratischer Papierbögen. Keines der Blätter ist gefaltet, markiert oder eingeschnitten. Die Blätter können unterschiedlich groß sein. Die Linien, die das Muster zeigt, sind die Ränder der Blätter. Wie viele Bögen Papier liegen mindestens auf dem Stapel?
Man braucht mindestens acht Blatt Papier, um das Muster zu erzeugen. Die rechteckigen Felder können nicht Teile von Blättern sein, die in dem Stapel ganz oben liegen. Am einfachsten beginnt man darum in dem Stapel ganz unten. Dort liegt das blaue 4×4-Quadrat A. In der nächsten Schicht befindet sich das 2×2-Quadrat B, das halb von 2×2-Quadrat C abgedeckt wird. Darauf liegt das grüne 3×3-Quadrat D und darauf wiederum das 2×2-Quadrat E. In der obersten Schicht liegen schließlich noch die drei 1×1-Quadrate F, G und H.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.