Ramanujan

Der geniale indische Mathematiker Srinivasa Ramanujan (1887–1920) erzählte einmal seinem Förderer Godfrey Harold Hardy von der vierstelligen Nummer eines Taxis und fand sie im Gegensatz zu dessen Meinung sehr bemerkenswert: Es sei nämlich die kleinste Zahl, die auf zwei Arten als Summe zweier (positiver) Kubikzahlen geschrieben werden könne. Wie viele gibt es davon überhaupt?
Die beiden vierstelligen Zahlen mit der genannten Eigenschaft sind 1729 und 4104. Wenn Sie nun die Zerlegung nicht im Kopf hinkriegen: Auch Ramanujan hatte das nicht spontan ausgerechnet, sondern sich gemerkt, wobei die Zahlen für ihn so etwas wie persönliche Bekannte waren.
Lassen Sie doch Ihren Computer eine Tabelle aufstellen!
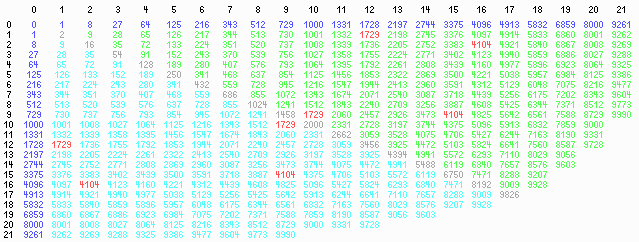
Die Tabelle zeigt alle bis zu 4-stelligen (natürlichen) Zahlen, die als Summen zweier Kubikzahlen auftreten, in rot die beiden, die es auf je zwei Weisen tun.
Welche natürliche Zahl ist die kleinste, die auf 2 bzw. auf 3 bzw. auf 4 Arten (Reihenfolge unbeachtet) als Summe von zwei Quadratzahlen auftritt?
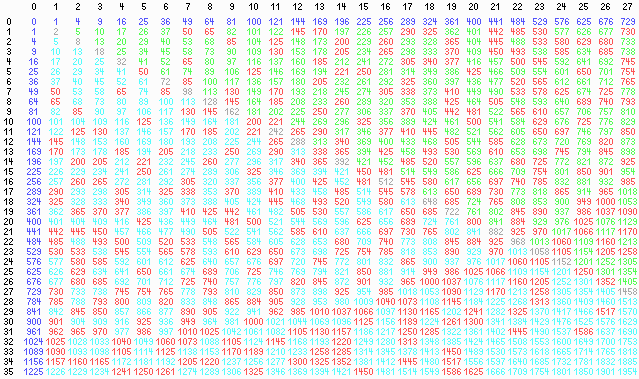
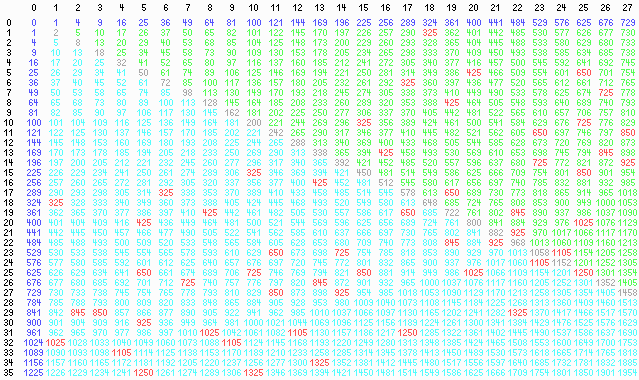
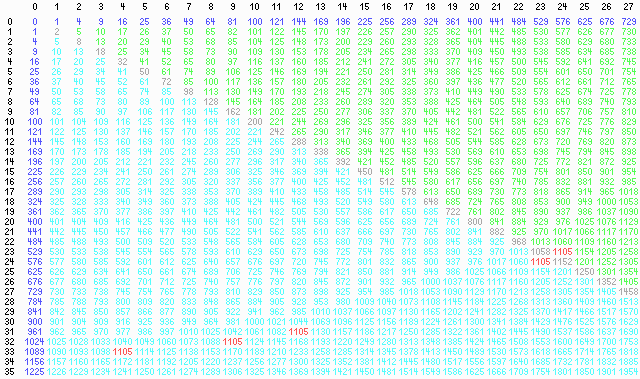




Schreiben Sie uns!
Beitrag schreiben