Roberval-Waage

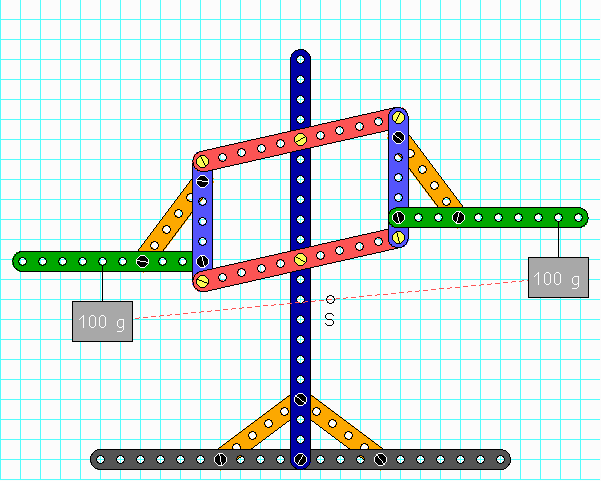
Dieses Bild zeigt die Seitenansicht eines seltsamen Gerätes. Die dunklen Schraubenköpfe gehören zu festen Verbindungen, die hellen Schraubenköpfe zu Drehlagern (nämlich mit zwei Muttern, die gegeneinander gekontert sind). Der Fuß wird z. B. mit einem Schraubstock festgehalten. Befindet sich die Waage im stabilen, im indifferenten oder in gar keinem Gleichgewicht?
Vergessen Sie alles über die Längen von Hebelarmen und bilanzieren Sie die Energie des Schwerefeldes bei einer möglichen Drehung der mittleren waagerechten Stangen, oder beachten Sie den gemeinsamen Schwerpunkt S der beiden Lasten.
Diese von Gilles P. de Roberval (1602–1675) erfundene Waage hat wegen ihrer Konstruktion mit dem halbierten Parallelogramm die Eigenschaft, dass die Lasten um einander entgegengesetzte Höhendifferenzen wandern können, unabhängig davon, an welchen Löchern sie befestigt sind. Sind die angehängten Gewichte gleich schwer, so ändert sich dabei nichts an der Energie des Schwerefeldes, das Gleichgewicht ist also indifferent, das heißt, es besteht bei jeder beliebigen Stellung der genannten Stangen.
Der gemeinsame Schwerpunkt der Lasten bleibt offensichtlich auf gleicher Höhe, und die Apparatur selbst ist symmetrisch.
Bei ungleichen Lasten besteht dagegen gar kein Gleichgewicht, die Waagebalken kippen bis zum Anschlag zu einer Seite.
Besonders gut kann die Waage mit einem Metallbaukasten (hier Märklin) gebaut werden, einige Stangen sind dabei doppelt.
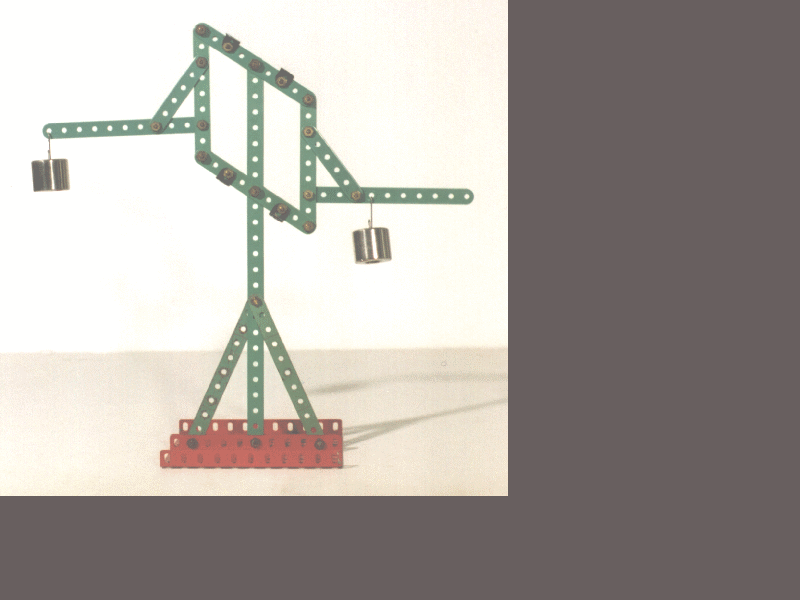
Auch mit "fischertechnik" geht es zu machen:

Dazu ein Video
Zusatzfrage
Wie kann man erreichen, dass man statt des indifferenten in der Mittellage ein stabiles (wie bei der alltäglichen Anwendung als Gemüsewaage!) oder auch ein labiles Gleichgewicht bei gleichen Lasten bekommt? Das abgebildete Märklin-Modell hat dazu bereits einige Häkchen.
Wird ein mehr oder weniger schweres Zusatzgewicht angebaut, das sich mitdrehen muss, so bekommt man bei gleichen Lasten ein stabiles Gleichgewicht, wenn der Schwerpunkt des Zusatzgewichts im unteren Scheitel eines Kreises liegt und der gemeinsame Schwerpunkt aller beweglichen Teile ebenfalls, aber im unteren Scheitel eines anderen Kreises. Bei (etwas) ungleichen Lasten gibt es ein stabiles Gleichgewicht bei einer kleinen Winkel-Auslenkung. Dann ist der gemeinsame Schwerpunkt wieder in einem unteren Scheitel, der des Zusatzgewichtes allein aber nicht.
Der gemeinsame Schwerpunkt des Zusatzgewichtes und der Lasten (also aller unsymmetrischen Teile) wandert hier auf einem Kreisbogen. Er liegt in dessen unterem Scheitel bei Waagerechtstellung der Waage.
Was geschieht, wenn das Zusatzgewicht einen Bogen nach oben durchläuft?
Baut man das Zusatzgewicht so an, dass es den oberen Scheitel eines Kreises durchlaufen kann, so bekommt man ein labiles Gleichgewicht bei Lastengleichheit und schon bei kleiner Ungleichheit eine eindeutige Anzeige des Vorzeichens der Differenz, nämlich eine Drehung bis zum Anschlag.
Hier wandert der gemeiname Schwerpunkt der Lasten und des Zusatzgewichtes auf einem Kreisbogen. Bei Waagerechtstellung der Waage liegt der Schwerpunkt im oberen Scheitel.
Bei einer Waage ist fast immer das stabile Gleichgewicht erwünscht, oft ist der Zeiger ("Zünglein") trotzdem oben, aber sein Gewicht wird durch ein größeres auf der Gegenseite (unten) übertroffen. Der Zeiger wandert dann auf die Seite mit der größeren Last.
Vor einigen Jahrzehnten wurde die Rolle einer kleinen Gruppe von Abgeordneten, insbesondere die einer kleineren Koalitionsfraktion, oft als "Zünglein an der Waage" beschrieben. Meistens war das in dem freundlichen Sinn gemeint, dass diese wenigen Leute angeblich die Entscheidung herbeiführen. Unfreundlicher wurde der gemeinte Sachverhalt aber auch so beschrieben: Der Schwanz wedelt mit dem Hund. Bei dem Bild mit dem Zünglein wurden aber Ursache und Wirkung verwechselt: Das Zünglein entscheidet bei der Waage nicht, wo es lang geht, sondern schlägt sich auf die Gewinnerseite, nicht viel anders als eine Wetterfahne oder jemand, der den Mantel nach dem Wind dreht.
Was ist nun von dieser Variante zu halten?
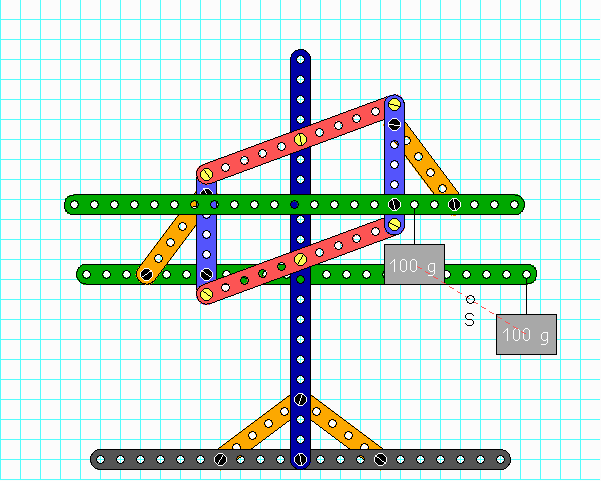
Hier muss man die Schrauben etwas länger machen, damit sich die Stangen nicht ins Gehege kommen, aber eigentlich ist sonst alles wie gehabt:
Die Roberval-Waage ist für mich das Musterbeispiel dafür, wie ein Gerät zunächst sehr verblüffend ist und sich dann als Beispiel für die Überlegenheit eines modernen Erklärungsmusters erweist: Mit der Energiebilanz kann man alle statischen (und auch hydrostatischen) Gleichgewichte sehr übersichtlich beschreiben und vorhersagen, wogegen die traditionelle Argumentation mit Kräften oder Drehmomenten, die als Ursachen aufgefasst werden, für jede "einfache Maschine" jeweils spezielle Aussagen machen muss, die dann sehr verschieden aussehen und manchmal nur mit Tricks anwendbar sind.
Die Physik erklärt zwar unverständliche Erscheinungen mit unverständlichen Naturgesetzen, aber ihre Eleganz besteht darin, dass sie viele Millionen von Erscheinungen mit wenig Dutzend Gesetzen beschreibt. Im Falle der einfachen Maschinen (d. h. der Geräte mit einem Freiheitsgrad – hier ein Drehwinkel) ist die zentrale Aussage: Wenn bei Änderung der Position (hier des Drehwinkels) die Summe aller potenziellen Energien konstant bleibt, ist das Gerät im indifferenten Gleichgewicht. Die Wippe, die Briefwaage und der Flaschenzug [mit vernachlässigten Seilmassen] sind damit eben so erfasst wie die Roberval-Waage.
Vor etwa 20 Jahren wurde ich durch einen Kollegen auf das Rätsel aufmerksam gemacht, der zugab, dass er das Ganze erst für einen Aprilscherz hielt, als jemand ihm einen Artikel darüber eingereicht hatte.




Schreiben Sie uns!
Beitrag schreiben