Satz von Ceva

In einem Dreieck verlaufen drei Geraden von je einer Ecke zu einem Punkt der jeweils gegenüber liegenden Seite. Sie teilen diese Seiten in die rundherum (vgl. Bild) als a b c d e f bezeichneten Teile.
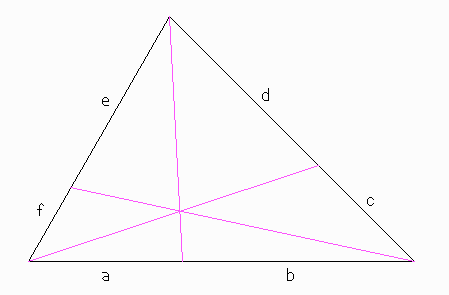
Man beweise: Wenn sie sich in einem gemeinsamen Punkt schneiden, ist
(a/b)·(c/d)·(e/f) = 1.
Tipp zum Flächenbeweis für Ceva
Suchen Sie Verhältnisse von Flächen, die jeweils einen Seitenteil als Grundseite und eine Ecke bzw. den Ceva-Schnittpunkt als Spitze haben.
Tipp zum physikalischen Beweis für Ceva
Schwerpunkt, aber nicht von der Fläche.
Geometrischer Beweis zum Satz von Ceva
Eine unserer drei Geraden teilt das blaue Teildreieck im Verhältnis a:b und den Rest des ganzen Dreiecks ebenfalls in diesem Verhältnis in das grüne und das gelbe Dreieck.
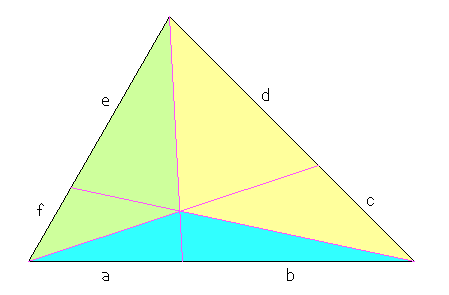
Entsprechend verhalten sich blau:grün wie c:d und gelb:blau wie e:f. Multipliziert man die drei Verhältnisse, so fallen die durch Farben gekennzeichneten Flächen heraus und es bleibt die Behauptung (a:b)·(c:d)·(e:f) = 1.
Satz von Ceva, mit physikalischer Deutung bewiesen
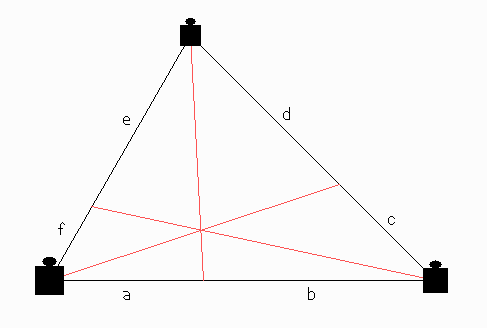
Denken Sie sich 3 verschieden schwere Punktmassen an den Ecken des Dreiecks. Die Geraden von einer Ecke zum Schwerpunkt der jeweils anderen beiden treffen sich in dem Schwerpunkt aller drei Ecken.



Schreiben Sie uns!
Beitrag schreiben