Scheimpflug

Eigentlich denkt man sich bei der Abbildung mit der Linse (zum Beispiel beim Fotografieren) die Ebenen von Objekt, Linse und Bild immer parallel. Wenn das aber nicht der Fall ist?
Von dem österreichischen Offizier und Kartographen Theodor Scheimpflug (1865–1911) stammt die folgende Regel: Man kann ein ebenes Objekt mit einem Objektiv (wir rechnen mit einer idealen dünnen Linse) scharf (im Allgemeinen allerdings verzerrt) abbilden, wenn Objektebene, Filmebene und Linsenebene sich in einer gemeinsamen Geraden schneiden. Wieso?
Gehen Sie von der idealen Abbildungsgleichung der dünnen Linse \(1/f = 1/g + 1/b\) aus. Nehmen Sie dann einen Objektpunkt auf einer Geraden an, die die optische Achse schneidet, geben Sie den Bildpunkt dazu an und zeigen Sie, dass er auf einer Geraden (bzw. Ebene) durch die genannte Gerade (im Schnitt mit der Zeichnungsebene durch den entsprechenden Punkt) geht.
Wir nennen die Höhe, in der die Objektebene die Linsenebene schneidet, \(h\) und die Objektweite, die in der optischen Achse vorliegt, \(a\). Dann wählen wir einen Objektpunkt in unserer Zeichenebene, dessen Lage (noch) von dem einzigen Parameter \(x\) abhängt, und zwar so, dass seine Weite (Entfernung von der Objektivebene) \(g = a\cdot x\) und die Gegenstands(punkt)höhe \(G = h\cdot(1 – x) \) sind. Wenn nun der Bildpunkt auf einer Geraden durch den Schnittpunkt aus Zeichenebene, Linsenebene und Objektebene (oben in der Zeichnung) liegen soll, darf das Verhältnis \((B + h)/b\) nicht von \(x\) abhängen.
Wir setzen darum \(g\) und \(G\) in die Abbildungsgleichung \(1/f = 1/g + 1/b\) ein und finden \(b = f a x /(a x – f)\) und \(B = G b/g = (f h – x f h)/(a x – f)\). Das gesuchte Verhältnis ist dann \((B + h)/b = h (a – f)/(a f)\) und hängt, wie verlangt, nicht von \(x\) und damit der Position des Objektpunktes auf der (geneigten) Objektebene ab. Aus diesem Verhältnis findet man ohne weiteres den Schnitt der Bildebene mit der optischen Achse bei der speziellen Bild(punkt)weite \((a f)/(a – f)\), die natürlich zu dem Objektpunkt mit der Weite \(a\) gehört, wie es die Abbildungsformel bestätigt.
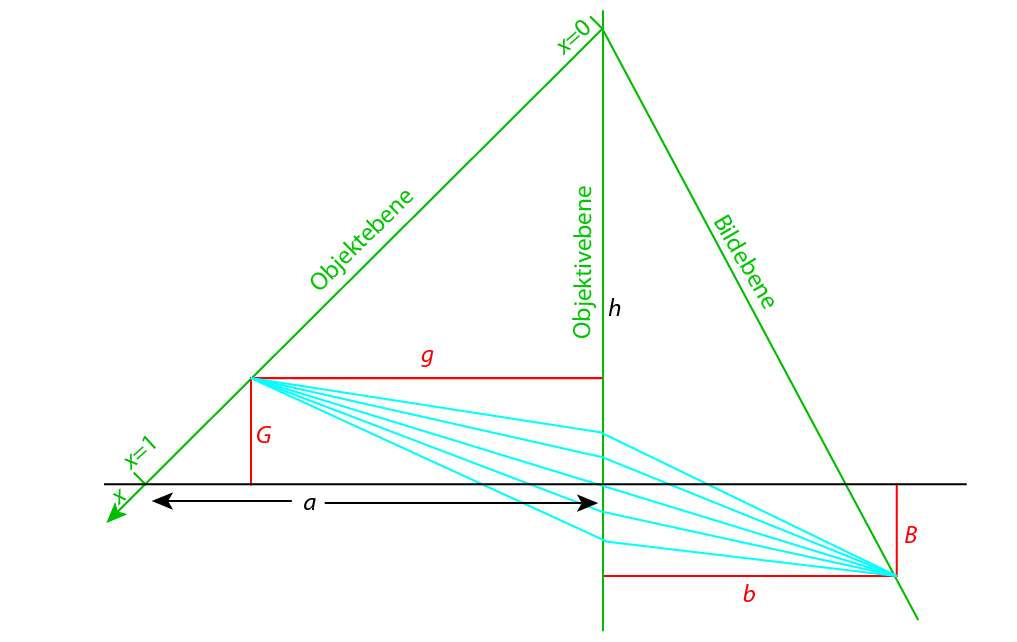
Im Prinzip kann man nach diesem Verfahren z. B. senkrechte Fassaden aus der Froschperspektive aufnehmen, ohne sich Sorgen um die Schärfentiefe zu machen, und im Labor am Vergrößerungsgerät wieder entzerren. Die Objektivebene muß in beiden Fällen durch die Schnittlinie aus Objekt- und Bildebene gehen. Man benötigt allerdings eine Kamera, bei der man entweder das Objektiv oder die Film (bzw. dann eher Platten-)halterung gegen das Gehäuse verkippen kann.
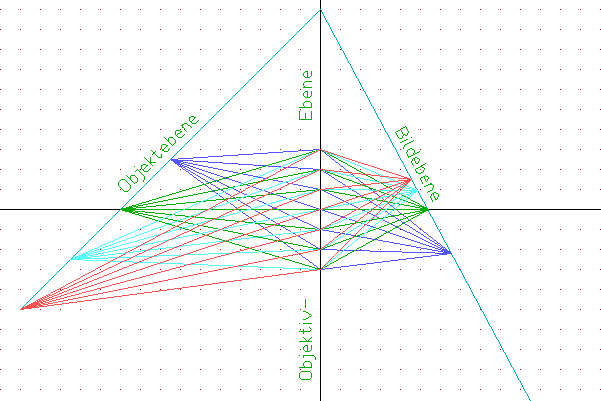
Dazu eine Animation:



Schreiben Sie uns!
Beitrag schreiben