Siebeneck
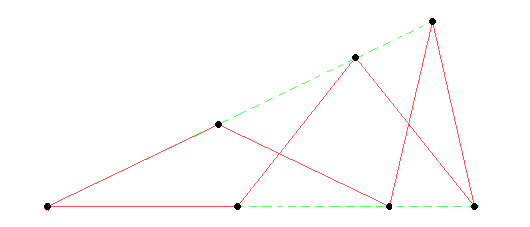
Dieses gleichseitige Siebeneck

ist so überschlagen, dass seine Ecken auf zwei sich schneidende Geraden verteilt sind. Wie groß ist der Winkel zwischen diesen?

Bestimmen Sie die Winkel der Reihe nach als Vielfache des gesuchten und benutzen Sie dazu die gleichschenkligen Dreiecke.
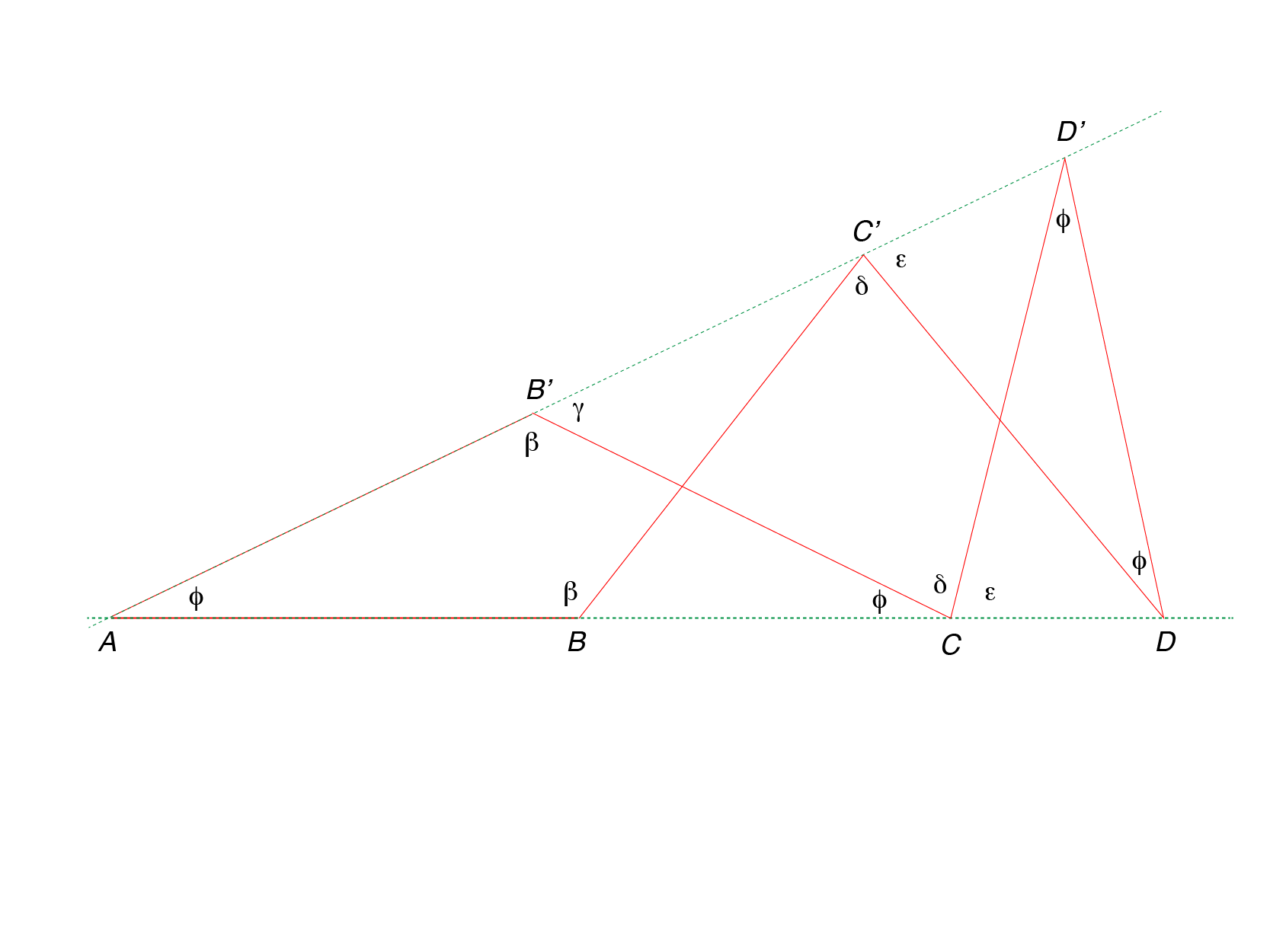
Der gesuchte Winkel ist \(\phi\). Die Dreiecke \(ADD'\) und \(DD'C\) sind ähnlich, daher sind die eingezeichneten Winkel bei \(D\) und \(D'\) ebenfalls gleich \(\phi\). Man nutzt, dass zahlreiche Dreiecke gleichschenklig sind, und findet \(\beta = \pi-2\phi\) (in Dreieck \(ACB'\)), \(\gamma=\pi-\beta=2\phi\) (Nebenwinkel bei \(B'\)), \(\delta=\pi-2\gamma=\pi-4\phi\) (in Dreieck \(B'CD'\)), \(\epsilon = \pi-\delta-\phi=3\phi\) (Nebenwinkel bei \(C\)). Außerdem ist \(\epsilon=(\pi-\phi)/2\) (in Dreieck \(CDD'\)). Aus den letzten beiden Gleichungen errechnet man \(\phi=\pi/7\approx 25,714^\circ\). Wie üblich bezeichnet \(\pi\) (im Bogenmaß) den gestreckten Winkel von 180o.
Man kann aus der Figur durch rotationssymmetrische Ergänzung dieses schöne 14-Eck mit zwei Systemen aus Rauten machen, alle mit ganzzahligen Vielfachen dieses Winkels:

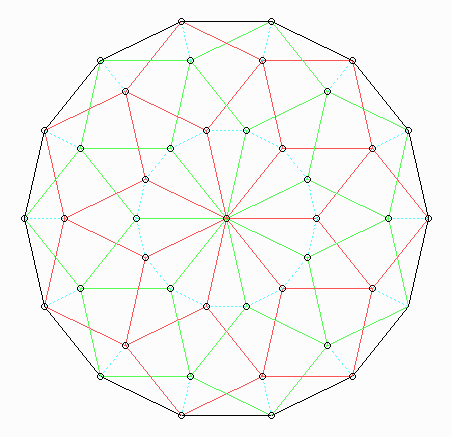
So haben zwei Mathematiker in Siracusa (wo früher kein Geringerer als Archimedes gewohnt hat) mit zwei Weinkarten (mit geraden Kanten!) und sieben Zahnstochern (alle gleich lang!) das Problem gelöst, wie man ein regelmäßiges 7-Eck (mit einem 14-Eck zwischendurch) ohne Winkelmesser zeichnen kann. Das berichtet jedenfalls der Maler Crockett Johnson in der Math. Gaz. 59(1975)17-21 und verweist dabei aber auch auf die Mathematical Note 2863 der Gazette (Math. Gaz. 43(1959)199) von Archibald H. Finlay, die die allgemeine Lösung der überschlagenen \(n\)-Ecke zwischen den sich schneidenden Geraden zeigt.
Geht das auch für andere Zahlen als 7?
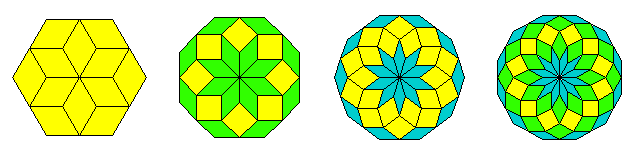
Hier sind die ungeraden Zahlen \(n\) = 5, 7, 9, und 11:
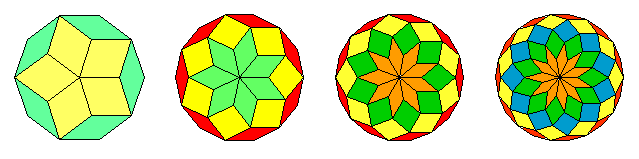
Sie liefern regelmäßige \(2n\)-Ecke mit \((n-1)/2\) verschiedenen Rauten, deren Winkel jeweils ganzzahlige Vielfache von 180o/\(n\) sind.
Für die geraden Zahlen \(n\) = 6, 8, 10 und 12 gibt es nur \(n\)-Ecke, da je zwei der erwarteten Seiten ohne Knick aneinander grenzen. Die Rautenarten werden hier ebenfalls durch die Farben angezeigt.
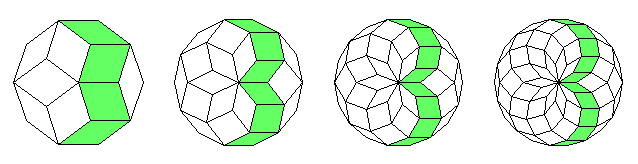
Man kann die Rauten auch zu Bändern zusammenfassen, bei denen jeweils eine Seitenrichtung gleich bleibt:
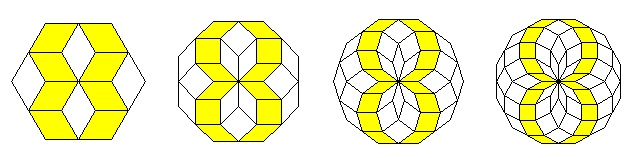
Man findet Spiralstrukturen:
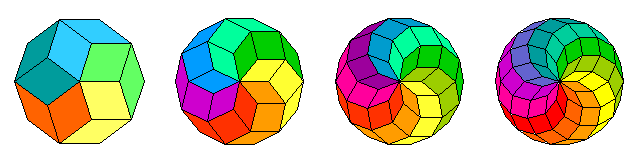
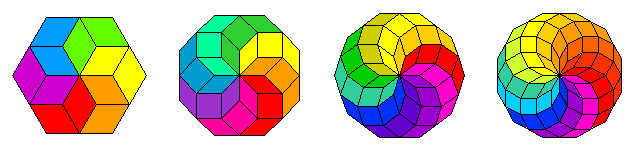
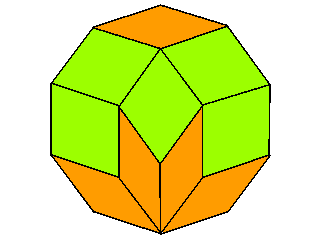
Am Beispiel des Zehnecks ist hier zu sehen, dass die Rauten auch verschieden gelegt werden können:
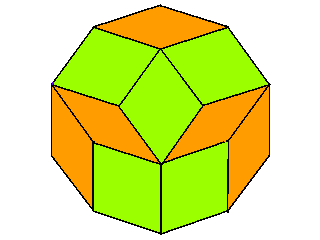
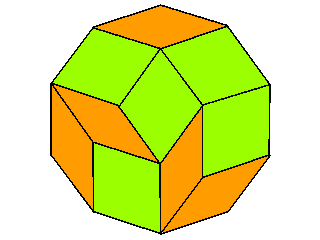
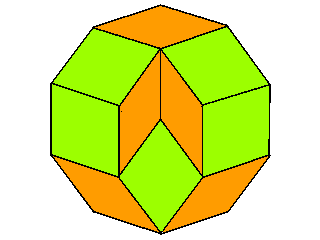
Ebenso ist es beim 12-Eck, in dem 3 Quadrate auftreten:
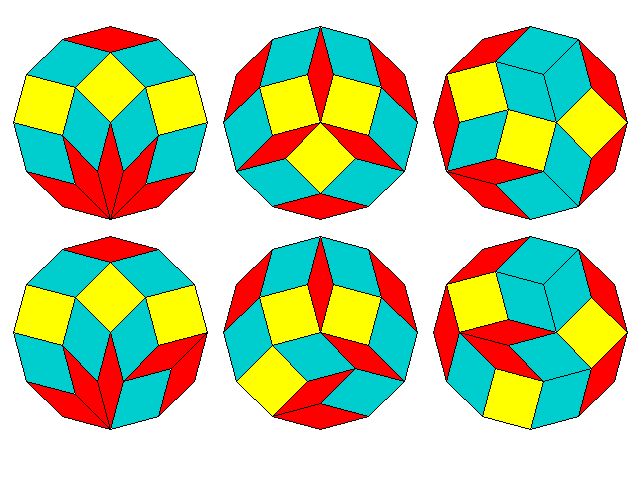
In diesem Tableau für \(n\) = 3 bis 14 zeigen gleiche Farben jeweils gleiche Rautenarten (d. h. Winkel) an, die Zahlen bezeichnen die tatsächliche Zahl der Ecken:
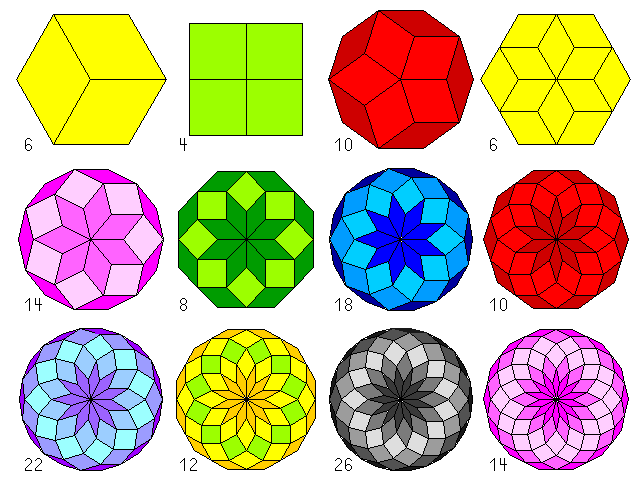
Für \(n = 25\) gibt es ein 50-Eck, das zumindest bei dieser Färbung den räumlichen Eindruck eines Torus macht:

Man kann aber auch Teile von ihm färben, so dass ein 26-Eck zu sehen ist, oben radial gefärbt, unten azimutal:

Das in Rauten zerlegte 12-Eck ist auch bei Lindgren am Schluss von Abschnitt 21 zu sehen, aber leider nicht bunt.
Heinz Klaus Strick hat hier gezeigt, wie man diese Füllungen des \(2n\)-Ecks als Projektionen eines rechtwinkligen Gitters aus dem \(n\)-dimensionalen Raum auffassen kann.



Schreiben Sie uns!
Beitrag schreiben