Skulpturenpark

Im Skulpturenpark des Kunstmuseums gibt es genau quadratische Inseln zwischen einigen flachen Teichen. Drei Inseln haben die Flächen \(74 \,{\rm m}^2\), \(116 \,{\rm m}^2\) und \(370 \,{\rm m}^2\). Sie grenzen mit den Ecken aneinander. Welche Fläche hat der dreieckige Teich zwischen ihnen?
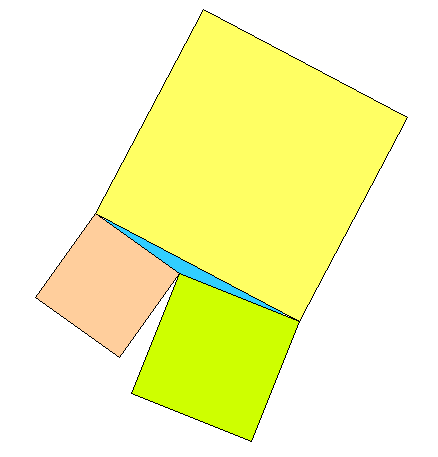
Die Berechnung geht ganzzahlig auf, und man braucht keine Trigonometrie.
Man kann die Aufgabe (mit einer Skizze, die man sich malen sollte) fast im Kopf erledigen, wenn man bemerkt, dass alle drei genannten Zahlen Summen von zwei Quadratzahlen sind.
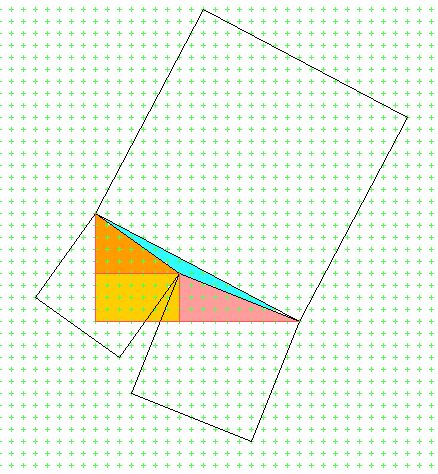
\(74=7^2+5^2, 116=10^2+4^2, 370=17^2+9^2\)
Anhand der Rasterpunkte kann man leicht abzählen, dass die Differenz aus den rechtwinkligen Dreiecken und dem Rechteck \(11 \,{\rm m}^2\) ist. Oder, wenn man schon die Koordinaten hat, stellt man fest, dass das gesuchte Dreieck die Hälfte des Parallelogramms aus den Vektoren (10, –4) und (–7, 5) ist, und dessen Fläche ist über das Kreuzprodukt schnell berechnet.
Bei Dudeney (Nr. 189) und bei Sam Loyd (1/36) handelt diese Aufgabe bei gleichen Zahlen, aber größeren Flächeneinheiten von landwirtschaftlichen Flächen.



Schreiben Sie uns!
Beitrag schreiben