Das Dreieck 3-4-5

Ein Gartenlokal ist mit einem Zaun aus gleich langen Stücken umgrenzt, die man nur mit den Enden aneinander stecken kann, und zwar hat es die Form eines rechtwinkligen Dreiecks mit 3, 4 und 5 solchen Stücken als Seitenlängen.
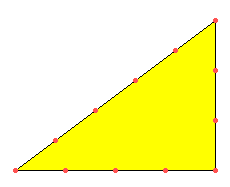
Man kann das Folgende auch als Streichholz-Legeaufgabe auffassen, wenn man die Spielregeln in diesem Sinne festlegt:
Die Fläche soll mit zusätzlichen Stücken genau dieser Längen (und mit Kontakt nur an den Enden der Stücke) unterteilt werden, und zwar:
- mit 3 Stücken im Verhältnis (1/6):(1/3):(1/2),
- mit 2 Stücken im Verhältnis (1/2):(1/2),
- mit 4 Stücken im Verhältnis (1/3):(1/3):(1/3),
Was hat der Inkreisradius mit der Fläche zu tun?
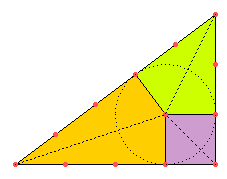
Die Lote vom Inkreismittelpunkt auf die Seiten teilen unser Dreieck im Verhältnis (1/6):(1/3):(1/2).
Dass der Inkreisradius genau eine unserer Längeneinheiten lang ist, sieht man (erst gar nicht und dann sofort) ein, wenn man die Fläche von 6 Quadrateinheiten (entlang der gestrichelten Linien im Bild) in drei Teile mit je einer Seite als Grundseite und dem Inkreisradius als Höhe aufteilt.
Wer hätte das gedacht, dass eins der berühmtesten Dreiecke (wenn man so sagen darf) einen so glatten Wert für den Inkreisradius hat!
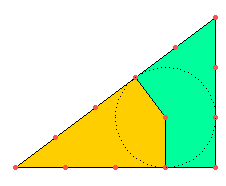
Es ist schon erstaunlich, wie einfach man das Dreieck halbieren kann, und mit dem Bisherigen ist es auch klar, wieso.
Und nun noch dritteln: Das ist auch nicht schwer, wenn auch eher selten als schön:
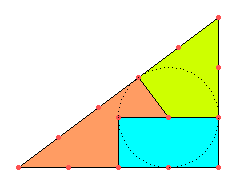



Schreiben Sie uns!
Beitrag schreiben