Das Wohnzimmer des Leuchtturmwärters

Der Leuchtturmwärter hat ein Wohnzimmer, das als Grundriss einen konzentrischen Kreisring hat. Neulich bekam er einen Teppichboden für die ganze Fläche geliefert, aber leider hatte niemand die Radien der beiden Kreise aufgeschrieben, und so konnte man die Fläche nicht für die Bestimmung des Lieferpreises bestimmen.
Zum Glück wusste der Azubi des Teppichhändlers Rat: Er hatte nämlich eine 6 m lange dünne, aber gerade Latte gesehen, die irgend wann einmal zugleich mit den Enden die runde Außenwand und mit der Mitte die Innenwand berührt hatte.
Wie groß ist die Teppichfläche? Wenn Sie glauben, dass man die Fläche wirklich eindeutig aus den gegebenen Daten berechnen kann, ist es besonders einfach, aber auch sonst nicht schwer.
Wenn man mit Unbekannten rechnet, kann es passieren, dass es plötzlich weniger werden.
Wenn die Fläche wirklich nur von der Länge dieser Latte und nicht von den beiden Radien abhängt, muss die Rechnung auch für den Grenzfall gelten, dass der innere Radius = 0 ist, und die Fläche ist dann die eines Kreises mit 6 m Durchmesser, also \(\pi \cdot 9 \; {\rm m}^2.\)
Wenn wir aber misstrauische Menschen sind, wollen wir das ohne die Annahme einsehen:
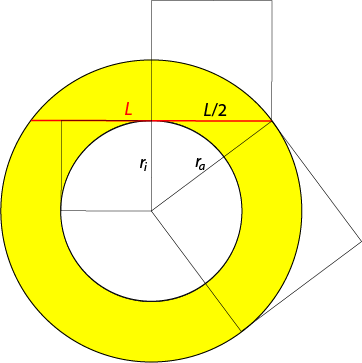
Das Bild zeigt den Ring mit der Latte. Deren halbe Länge \(L\,/\,2\) bildet mit den beiden Radien \(r_a\) und \(r_i\) ein rechtwinkliges Dreieck, und es gilt für die Fläche \(A =\pi\cdot(r_a^2 – r_i^2) = \pi\cdot(L\,/\,2)^2\).
Die Sache mit den scheinbar unvollständigen Daten hatten wir schon einmal in drei statt zwei Dimensionen: beim Serviettenring.



Schreiben Sie uns!
Beitrag schreiben