Steiner-Ellipsen
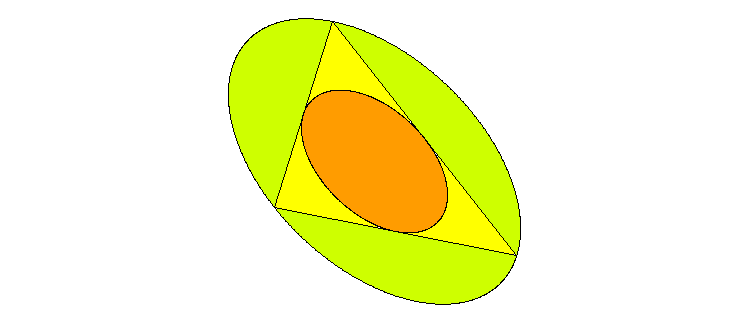
Zu einem beliebigen ebenen Dreieck sollen zwei Ellipsen gezeichnet werden, und zwar die größte, die ganz hineinpasst, und die kleinste, in die das Dreieck passt. Wie verhalten sich ihre Flächen zueinander?
Fangen Sie mit einem gleichseitigen Dreieck an.
Für das gleichseitige Dreieck sind die beiden Ellipsen Kreise und nicht schwer zu finden. Verzerren Sie nun die ganze Figur affin.
Was ist eine affine Abbildung? In der Ebene – die uns hier interessiert – ist es eine Translation gefolgt von einer linearen Abbildung. Diese wiederum kann man auffassen als eine Kongruenzabbildung gefolgt von einer Verzerrung, bei der alle Punkte in zwei verschiedenen, nicht notwendig zueinander rechtwinkligen Richtungen mit verschiedenen Faktoren vom Nullpunkt weg gestreckt oder auch den Nullpunkt zu gestaucht werden. Jedes Dreieck lässt sich durch eine affine Abbildung in jedes andere verwandeln. Unter einer affinen Abbildung bleiben Verhältnisse von zueinander parallelen Strecken und von Flächen gleich, und Ellipsen bleiben Ellipsen. Die vielen Mittelpunkte des Dreiecks, die beim gleichseitigen Dreieck alle zusammenfallen, gehen dabei getrennte Wege. Wegen der Streckenverhältnisse behält allerdings einer der Mittelpunkte seine Rolle auch bei der Verzerrung. Die Mittelpunkte von Umkreis und Inkreis sind es offensichtlich nicht.
Es ist der Schwerpunkt! Beide Ellipsen sind ähnlich zueinander und haben ihre Mittelpunkte im Schwerpunkt des Dreiecks. Die kleine Ellipse berührt das Dreieck in den Seitenmitten, die Flächen beider Ellipsen verhalten sich wie 4:1. Die große Ellipse heißt Steiner-Umellipse nach Jakob Steiner (1796–1863), dem Mathematiker, dem wir unter anderem den Steiner-Baum verdanken.
Schreiben Sie uns!
Beitrag schreiben