Hemmes mathematische Rätsel: Streichholzdreiecke
1848 erfand der Frankfurter Chemiker Rudolf Christian Boettger das Sicherheitszündholz. Doch niemand in Deutschland wollte seine Erfindung haben. Sie wurde von Schweden aufgekauft und von Frans Lundström weiterentwickelt, der auch gleich die Schiebeschachtel dazu erfand. Nun traten Boettgers Sicherheitshölzer als Schwedenhölzer ihren Siegeszug um die Welt an. Mit der Verbreitung der Schwedenhölzer entstanden auch die ersten Streichholzrätsel.
Eines der besten Werke des 19. Jahrhunderts über mathematische Denksportaufgaben ist das 1880 erschienene Buch Mathematische Kurzweil. Es wurde von dem Leipziger Schuldirektor Louis Mittenzwey geschrieben. Bis 1918 wurden sieben Auflagen davon gedruckt, und 1955 erschien noch eine von Bruno Rüger überarbeitete 8. Auflage. In diesem Buch taucht erstmals folgendes Streichholzproblem auf, das sich seitdem zu einem Denksportklassiker entwickelt hat.
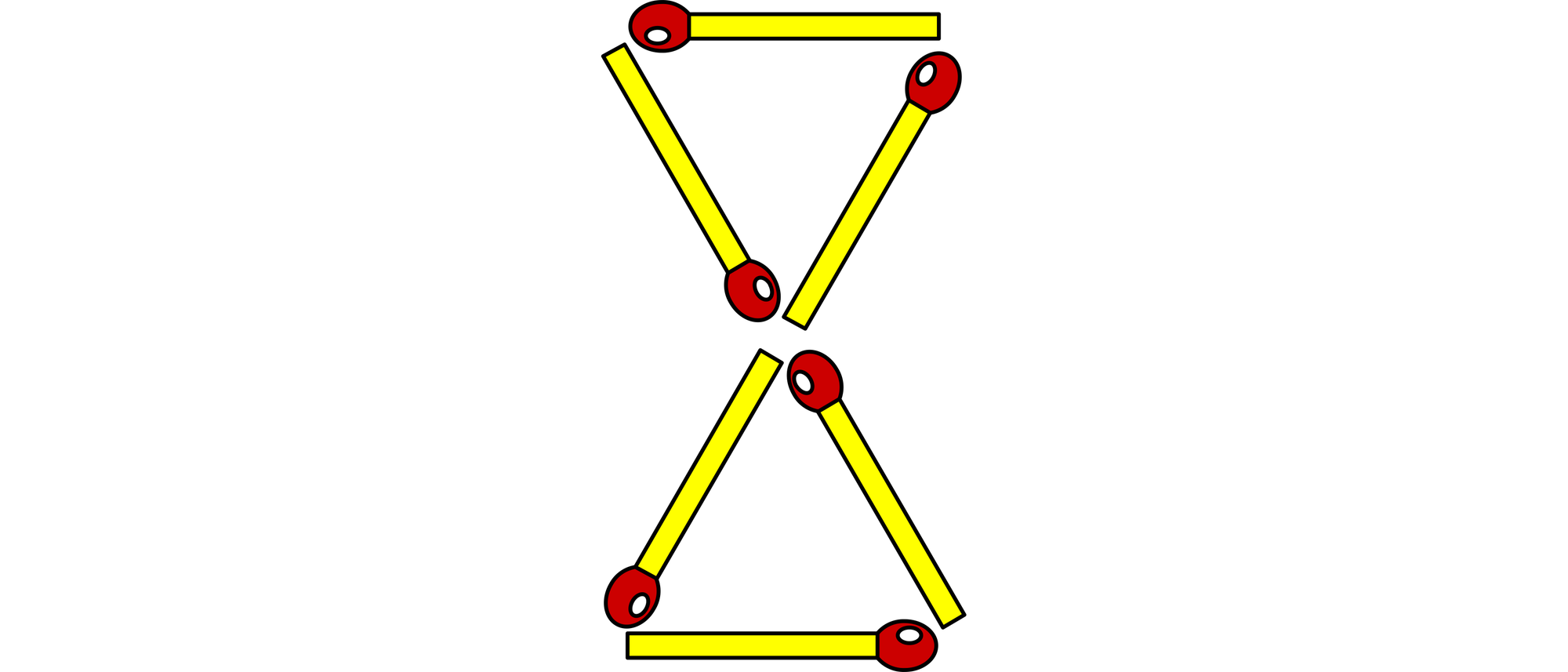
Sechs Streichhölzer bilden zwei gleichseitige Dreiecke mit einer Seitenlänge von einem Holz. Sie dürfen nun drei Hölzer in eine andere Position bringen. Danach sollen die sechs Streichhölzer vier gleichseitige Dreiecke bilden, deren Seiten alle ein Holz lang sind. Die Hölzer dürfen nicht gespaltet werden. Ist dies möglich?
Es gibt in der Ebene keine Möglichkeit, aus sechs Streichhölzern vier gleichseitige Dreiecke von einem Holz Seitenlänge zu legen. Aber es ist in der Aufgabe auch nicht verlangt worden, dass die vier Dreiecke in einer Ebene liegen müssen. Weicht man in die dritte Dimension aus, ist die Lösung leicht zu finden. Die sechs Streichhölzer werden zu einer Pyramide mit dreieckiger Grundfläche zusammengestellt.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.