Symmetrie von Polyedern
Wie viele Symmetrieachsen und Spiegelebenen hat ein Würfel, wie viele ein reguläres Oktaeder?
Bedenken Sie, dass das duale Polyeder zum Würfel ein reguläres Oktaeder ist. Orientieren Sie den Würfel und das Oktaeder so zueinander, dass die Dualität (vor allem die Entsprechungen zwischen Ecken und Flächen und zwischen Kanten und Kanten) zum Tragen kommt.
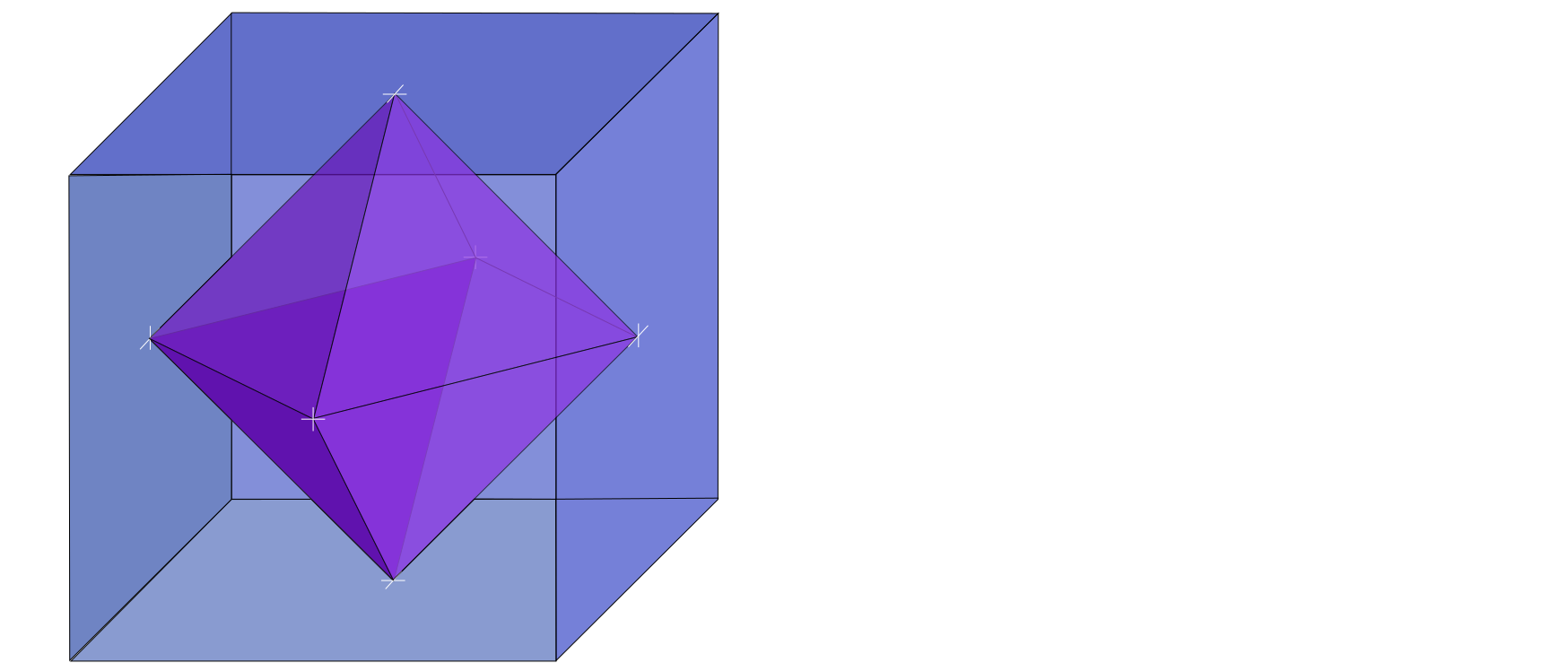
Hier haben wir den Würfel und das Oktaeder so in einem Bild, dass ihre Dualität deutlich wird:
Mit "Paar" ist im Folgenden stets ein zur Mitte punktsymmetrisches Paar gemeint:
Spiegelebenen
Parallel zu jedem der 3 Paare von Würfelflächen beziehungsweise zu jeder der 3 Äquatorebenen (aus je einem Diagonalenpaar) des Oktaeders gibt es eine Spiegelebene, wie in den Animationen dargestellt:
Zu jedem der 6 Paare von paralleler Würfelkanten gibt es eine Symmetrieebene (hier nur eine markiert):
Symmetrieachsen
Durch jedes der 4 Paare von Würfelecken beziehungsweise Oktaeder-Flächenmitten gibt es eine 3-zählige Achse:
Durch jedes der 3 Paare von Würfel-Flächenmitten oder Oktaeder-Ecken gibt es eine 4-zählige Achse:
Durch jedes der 6 Paare von Kantenmittelpunkten (von Würfel oder Oktaeder gleichermaßen) gibt es eine 2-zählige Achse:
Drei der Spiegelebenen und alle Achsen sehen dann so aus:
Es gibt also 13 Achsen und 9 Ebenen:
| 6 | - | Spiegelebenen | durch je 2 Kanten und 2 Diagonalen des Würfels | parallel zu je 2 Kanten des Oktaeders |
| 3 | - | Spiegelebenen | durch je zwei Diagonalen des Oktaeders | parallel zu Flächen des Würfels |
| 4 | 3-zählige | Achsen | durch Ecken des Würfels | durch Flächenmitten des Oktaeders |
| 3 | 4-zählige | Achsen | durch Flächenmitten des Würfels | durch Ecken des Oktaeders |
| 6 | 2-zählige | Achsen | durch Kantenmitten des Würfels | durch Kantenmitten des Oktaeders |
Andere reguläre und halbreguläre Polyeder
Der Würfel und das reguläre Oktaeder haben also 13 Achsen und 9 Ebenen. Das gilt dann auch für alle entsprechend symmetrisch ausgeführten Abstumpfungen zu Würfelstumpf, Oktaederstumpf, Kuboktaeder und zu dem kleinen und dem großen Rhombikuboktaeder und – allerdings nur für die Achsen-, nicht für die Ebenen-Symmetrie – zum Cubus simus. Auch der Übergang zum jeweils dualen Polyeder bewahrt die Symmetrie-Eigenschaften, also nicht nur der zwischen Würfel und Oktaeder, sondern auch von den archimedischen Stümpfen zu den Catalan-Polyedern, also zum Beispiel vom Kubokateder zum Rhombendodekaeder.
Wir können nun ein Schema der Symmetrie-Eigenschaften aller regulären und halbregulären Polyeder aufstellen:
Symmetrie regulärer und halbregulärer Polyeder | |||
12-er-Familie | 30-er-Familie | ||
spiegelsymm. | händig | spiegelsymm. | händig |
| Oktaeder, Würfel, Oktaeder-Stumpf, Würfelstumpf, Kuboktaeder, Kuboktaeder-Stumpf, Rhomben-Kuboktaeder und alle dazu dualen Catalan-Polyeder | Cubus simus und sein duales Catalan-Polyeder | Ikosaeder, Dodedaeder, Ikosaeder-Stumpf, Dodekaeder-Stumpf, Ikosidodekaeder, Ikosidodekaeder-Stumpf, Rhomben-Ikosidodekaeder und alle dazu dualen Catalan-Polyeder | Dodecahadron simum und sein duales Catalan-Polyeder |
| 3 vierzählige Achsen durch Oktaeder-Ecken bzw. Würfel-Flächenmitten und 3 Spiegelebenen rechtwinklig dazu | 3 vierzählige Achsen durch Oktaeder-Ecken bzw. Würfel-Flächenmitten | 6 fünfzählige Achsen durch Ikosaeder-Ecken bzw. Dodekaeder-Flächenmitten und 6 Spiegelebenen rechtwinklig dazu | 6 fünfzählige Achsen durch Ikosaeder-Ecken bzw. Dodekaeder-Flächenmitten |
| 4 dreizählige Achsen durch Oktaeder-Flächenmitten bzw. Würfel-Ecken | 10 dreizählige Achsen durch Ikosaeder-Flächenmitten bzw. Dodekaeder-Ecken | ||
| 6 zweizählige Achsen durch Oktaeder- bzw. Würfel-Kanten und 6 Spiegelebenen rechtwinklig dazu | 6 zweizählige Achsen durch Oktaeder- bzw. Würfel-Kanten | 15 zweizählige Achsen durch Ikosaeder- bzw. Dodekaeder-Kanten und 15 Spiegelebenen rechtwinklig dazu | 15 zweizählige Achsen durch Ikosaeder- bzw. Dodekaeder-Kanten |
| gesamt 13 Achsen und 21 Ebenen | gesamt 13 Achsen | gesamt 31 Achsen und 21 Ebenen | gesamt 31 Achsen |
Diese Tabelle erfasst alle regulären und halbregulären Polyeder, also die platonischen, archimedischen und catalanschen.
Oktaeder und Würfel sind zueinander dual und haben daher gleich viele Kanten, nämlich 12. Das entspricht auch der Eckenzahl des Kuboktaeders, den man aus dem einen wie aus dem anderen durch Abstumpfen bis zum Verschwinden der alten Kanten bekommt. Es gibt drei Arten von Achsen, für jede ist das Produkt aus ihrer Anzahl und ihrer Zähligkeit 12, nämlich: 3 mal 4, 6 mal 2, 4 mal 3. Die erste Art geht durch Ecken des Oktaeders oder Flächenmitten des Würfels, die zweite durch Kantenmitten, die dritte durch Flächenmitten des Oktaeders oder Ecken des Würfels. Zu der ersten und der dritten Sorte gibt es je eine zur Achse rechtwinklige Spiegelebene, außer in der Spalte für die händigen Polyeder.
Dasselbe gilt jetzt wörtlich, nur mit anderen Zahlen, für die rechten beiden Spalten, nämlich mit dem Produkt 30 statt 12 und mit der Zähligkeit 5 statt 4, denn das Ikosaeder und das Dodekaeder haben jeweils 30 Kanten (und ebenso viele Ecken hat das Ikosidodekaeder, das dem Kuboktaeder analog ist).
Die folgende Animation zeigt, wie das Ikosaeder, das Dodekaeder und das Ikosidodekaeder stellvertretend für die ganze 30-er-Familie gemeinsam um eine der 30 durch die Kantenmitten des Ikosaeders oder des Dodekaeders und durch die Ecken des Ikosidodekaeders gehenden Achsen rotieren.
Das Tetraeder, das zu seinem eigenen Punkt-Spiegelbild dual ist, sein Stumpf und das dazu duale Triakis-Tetraeder fallen aus diesem (bemerkenswert kompakten!) Schema heraus. Sie haben nämlich 4 dreizählige Achsen durch jeweils eine Ecke und die gegenüber liegende Flächenmitte, und 3 zweizählige Achsen durch die Mitten zweier sich gegenüber liegender Kanten. Durch jede der 6 Kanten (und natürlich den Mittelpunkt des ganzen Tetraeders) geht eine Spiegelebene.
Die Symmetrien des Tetraeders, seines Stumpfs und des Triakis-Tetraeders lassen sich folgendermaßen veranschaulichen: Die sechs Kreise stehen für die Spiegelebenen, und die Punkte zeigen den Schnittpunkt der Achsen mit den Kreisen.
Nun in ähnlicher Kugel-Darstellung die Symmetrie von Oktaeder, Würfel, Kuboktaeder und so weiter:
... und für Ikosaeder, Dodekaeder, Ikosidodekaeder und so weiter
Zum Abschluss noch ein Blick auf die unendlich vielen Prismen et cetera. Ein \(n\)-zähliges Prisma hat je ein regelmäßiges \(n\)-Eck als "Boden" und "Deckel" sowie \(n\) Quadrate als "Wände". Das \(n\)-Eck hat eine \(n\)-zählige Drehsymmetrie um seinen Mittelpunkt und \(n\) Spiegelachsen. Diese gehen bei ungeradem \(n\) durch jeweils eine Ecke und die gegenüberliegende Seitenmitte, bei geradem \(n\) dagegen durch jeweils zwei Ecken oder zwei Seitenmitten. Das zugehörige Prisma erbt von seinem \(n\)-Eck die \(n\)-zählige Drehsymmetrie. Aus jeder Spiegelung des \(n\)-Ecks wird erstens eine zweizählige Drehung um eine Achse, die genau in der Mitte zwischen den Spiegelachsen von Boden und Deckel verläuft, und zweitens eine Spiegelung an der vertikalen Ebene durch diese Achse. Schließlich gibt es noch die Spiegelung an der Mittelebene zwischen Boden und Deckel. Das macht insgesamt \(n+1\) Drehachsen und \(n+1\) Spiegelebenen. Dieselben Symmetrien wie die Prismen haben die (zu ihnen dualen) Doppelpyramiden.
Antiprismen der Zähligkeit \(n\) haben eine \(n\)-zählige ("vertikale") Drehachse, dazu \(n\) Spiegelebenen, die durch die genannte Achse sowie jeweils eine Symmetrieachse von Boden- bzw. Deckelpolygon definiert sind. Außerdem gibt es noch zweizählige Drehungen um Achsen, die von der Mitte einer schrägen Kante zur Mitte der gegenüberliegenden schrägen Kante verlaufen.
Falls ein Prisma oder Antiprisma "zufällig" platonisch ist (wie das vierzählige Prisma, besser bekannt als der Würfel, und das dreizählige Antiprisma, besser bekannt als das Oktaeder), so hat es natürlich die entsprechende höhere Symmetrie.
Schreiben Sie uns!
Beitrag schreiben