Überraschend rund
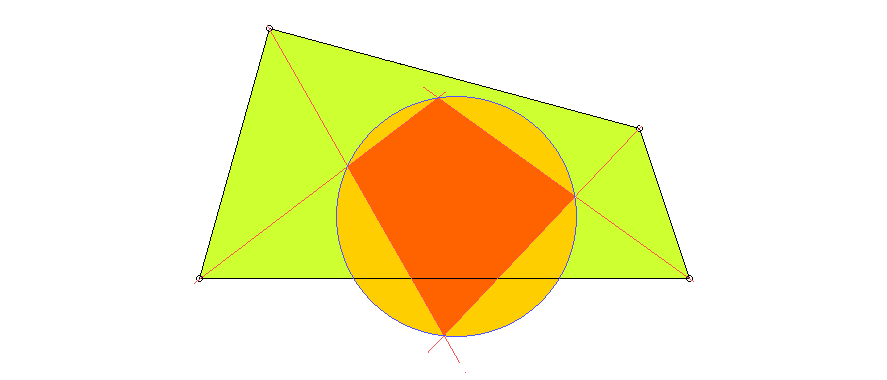
In diesem Viereck sind die Winkelhalbierenden gezeichnet. Ihre Schnittpunkte liegen auf einem Kreis. Ist das bei jedem ebenen Viereck so?
Winkelbilanz.
Das orangefarbene Viereck aus den Winkelhalbierenden enthält gegenüberliegende Paare von Winkeln, die sich zu jeweils zu 180° ergänzen. Aber warum?
Das erkennt man aus der Winkelbilanz der eingetragenen Dreiecke: Die zwei gegenüberliegenden Winkel des orangefarbenen Vierecks haben die Winkel \(180°-\alpha-\beta\) und \(180°-\gamma-\beta\). Deren Summe beträgt \(360°-\alpha-\beta-\gamma-\delta\).
Die Winkelsumme jedes Vierecks beträgt 360°, demnach gilt für das ursprüngliche grüne Viereck: \(2\alpha+2\beta+2\gamma+2\delta=360°\). Daraus folgt \(\alpha+\beta+\gamma+\delta=180°\), und damit beträgt auch die Summe der genannten gegenüberliegenden Winkel 180°. Den beiden anderen Winkeln bleibt dann nichts übrig, als sich ebenfalls zu 180° zu ergänzen. Also ist das orangefarbene Viereck ein Sehnenviereck und hat als solches einen Umkreis.
Honsberger bringt dies im Kapitel über Vierecke in seinen "Episoden".
Schreiben Sie uns!
Beitrag schreiben