Mit Hemmungen vorwärts!
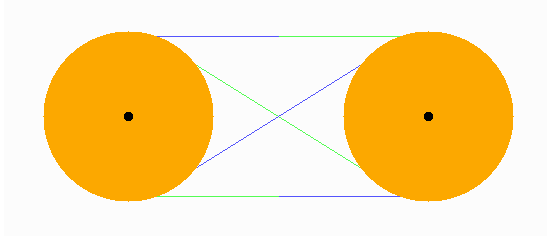
Hier sind zwei Rollen mit einem Seil umschlungen, dessen Hälften hier zur besseren Übersicht durch zwei Farben gekennzeichnet sind. Wie drehen sich die Rollen, wenn man das Seil mitten am unteren waagerechten Stück hält und waagerecht hin- und herbewegt?
Offenbar muss das Seil an einigen Stellen rutschen.
Die rechte Rolle dreht sich stets im Uhrzeigersinn, die linke diesem stets entgegen.
Wenn man in der Mitte des oberen waagerechten Seilstücks nach links oder rechts zieht, ist es genau umgekehrt. Aber warum?
Offenbar muss auf jeder Rolle jeweils ein Seilstück in dem einen Sinn und ein anderes in dem anderen herumlaufen. Wenn die Reibungskräfte überall gleich wären, könnten die Rollen dabei stillstehen.
Bewegt man beispielsweise eine Stelle des Seils nach rechts, lockert man die Seilspannung rechts von dieser Stelle und spannt es links von ihr etwas stärker. Damit kommt eine Asymmetrie in die Reibungskräfte, und die Hälfte der aufliegenden Seilstücke – die allesamt etwas länger als der halbe Rollenumfang, aber untereinander gleich lang sind – kann jeweils eine Rolle mitnehmen und ohne Gleiten auf ihr abrollen, während die anderen beiden Seilstücke gegen die Drehung der Rollen rutschen.
Wir haben also einen mechanischen Gleichrichter: Eine Schwingung (mit Hin- und Rückweg) wird in zwei Drehbewegungen gleicher Richtung übersetzt.
Basteltipp: Mit Fischertechnik kann man das Gerät gut mit zwei Paaren fest miteinander verbundener – also nur gemeinsam drehbarer – Rollen bauen, so dass das Seil in getrennten Rillen auf diesen Rollen laufen kann: zum Beispiel die unten waagerecht laufenden Seilstücke in den dem Betrachter zugewandten Rollen und die anderen in den hinteren, verdeckten.
Eine schöne Variante besteht auch in zwei Rollenpaaren mit zueinander rechtwinkligen windschiefen Achsen. Zum Beispiel verläuft eine Achse von oben nach unten, die andere von vorn nach hinten. Auf jeder Achse sind wieder zwei Rollen so montiert, dass sie sich nur gemeinsam drehen können. Diesmal aber haben die beiden Rollen den Abstand eines Rollendurchmessers voneinander. Die Seilstücke zwischen den Rollen bilden dann vier zueinander parallele Kanten eines (langen) Quaders, dessen Querseiten Durchmesser der Rollen sind.
Eine Apparatur von Cundy und Rollett ("A friction paradox" in "Mathematical Models", S. 210) arbeitet mit breiten Walzen und einem überkreuz verlaufenden Seil, läuft aber experimentell weniger gut.
Schreiben Sie uns!
Beitrag schreiben