Stoll
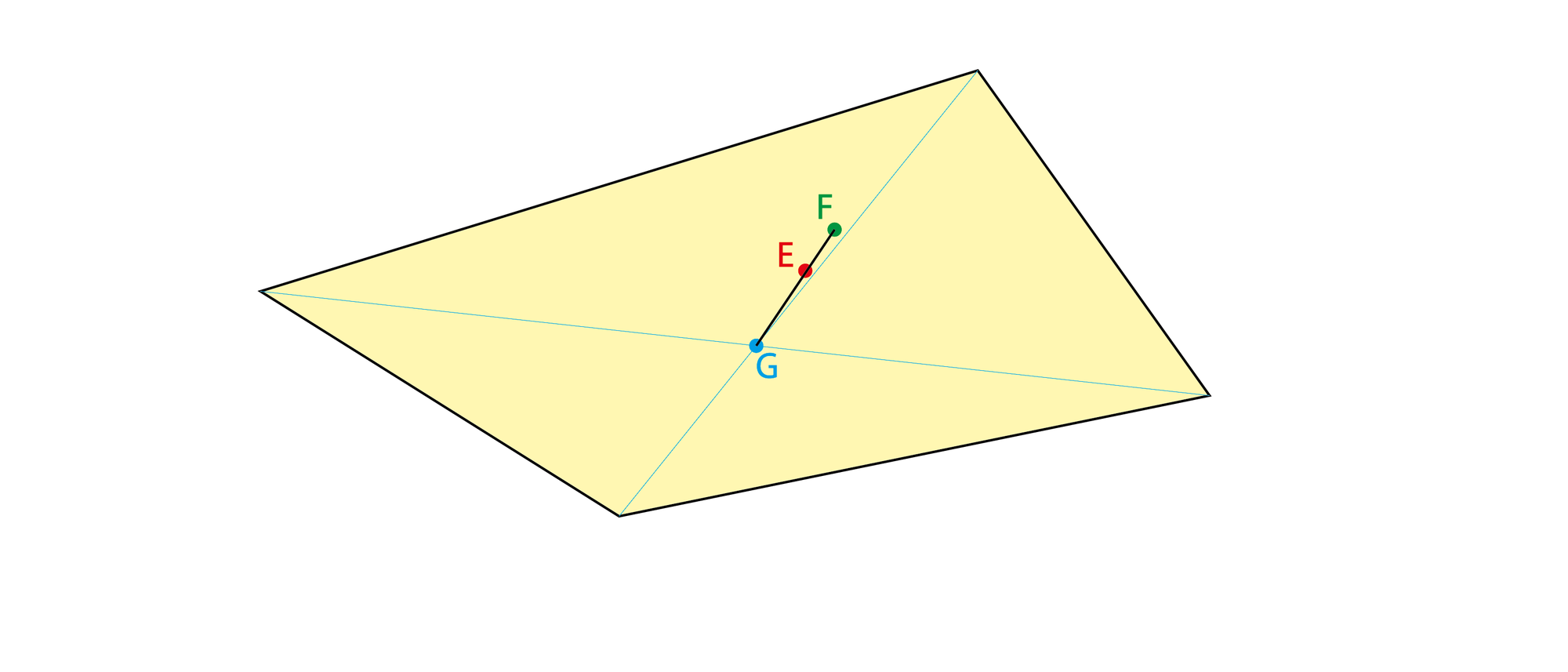
Im jedem ebenen (nicht überschlagenen) Viereck teilt der Eckenschwerpunkt E die Strecke zwischen dem Flächenschwerpunkt F und dem Diagonalenschnittpunkt G im Verhältnis 1/4 zu 3/4. Warum?
Zur Erinnerung:
- Der Eckenschwerpunkt in einem Viereck ist der Schnittpunkt der Seitenhalbierenden. (Beim Viereck sind die Seitenhalbierenden die Verbindungslinien der Mitttelpunkte gegenüberligender Seiten.)
- Um den Flächenschwerpunkt in einem Viereck zu berechnen, zerlegt man zunächst das Viereck durch eine Diagonale in zwei Dreiecke und ermittelt deren Eckenschwerpunkte (in Dreiecken sind Flächen- und Eckenschwerpunkt identisch). Der Flächenschwerpunkt des Vierecks liegt dann auf der Verbindungslinie dieser Schwerpunkte. Das gilt auch für die beiden Dreiecke, in die man das Viereck entlang der anderen Diagonale zerlegen kann. Der Schnittpunkt beider Verbindungslinien ist der Flächenschwerpunkt des Vierecks (vgl. das Rätsel "Wittenbauer").
Bestimmen Sie den Eckenschwerpunkt nach dem Schema 1 + 3 (und nicht 2 + 2, was normalerweise sinnvoller wäre).
In dem Viereck ABCD ist G der Schnittpunkt der Diagonalen, H und K sind die Mittelpunkte dieser Diagonalen, A– ist der (Ecken- oder Flächen-) Schwerpunkt des Dreiecks BCD, B– ist der Schwerpunkt des Dreiecks ACD und so weiter.
Die vier Dreiecksschwerpunkte dritteln die Strecke zwischen den Ecken und den Mittelpunkten der Diagonalen.
Der Eckenschwerpunkt E des Vierecks teilt die Strecke AA– im Verhältnis 3/4 zu 1/4, ebenso wie die Strecke BB– und so weiter. Die Begründung ist ganz physikalisch: In den Ecken A, B, C und D sitzen Massen der Größe 1. An deren Schwerpunkt ändert sich nichts, wenn man – zum Beispiel – die Massen von B, C, D in deren gemeinsamen Schwerpunkt A– verschiebt. Damit der "Waagebalken" AA– im Gleichgewicht ist, muss er so unterstützt werden, dass er im Verhältnis 3:1 geteilt wird, also im Punkt E.
Der Flächenschwerpunkt F des Vierecks ist der Schnitt von A–C– und B–D–.
C–A–CA ist ein Trapez mit dem Verhältnis 1:3 der parallelen Seiten, E ist sein Diagonalenschnittpunkt und hat daher (ähnliche Dreiecke) von AC den dreifachen Abstand wie von A–C–.
In gleicher Weise sieht man, dass E auch von BD den dreifachen Abstand hat wie von B–D–. Also teilt E die Strecke GF im Verhältnis 3/4 zu 1/4, wie in dem nach Stoll benannten Satz behauptet wird.
Schreiben Sie uns!
Beitrag schreiben