Pappos
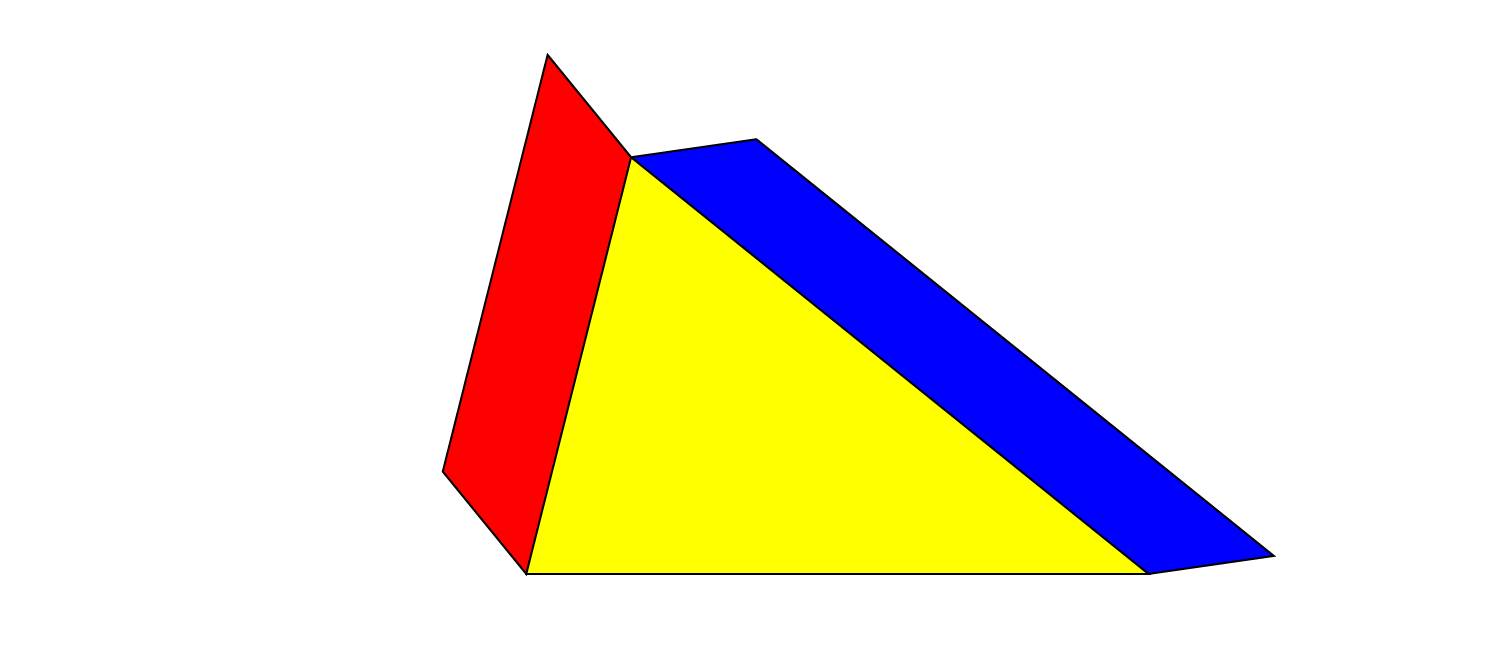
An zwei Seiten eines Dreiecks sind Parallelogramme angefügt. Wie konstruiert man ein Parallelogramm an die dritte Seite, dessen Fläche gleich der Summe der beiden anderen ist?
Scherung oder Versetzen von kleinen Dreiecken.
Zuerst verlängert man die äußeren Begrenzungen der Parallelogramme (dunkelblaue Linien). Ihren Schnittpunkt verbindet man anschließend mit der Ecke des Dreiecks und führt diese Linie nach unten fort (lila und grüne Linie). An den zwei anderen Ecken des Dreiecks zeichnet man Parallelen zu ebendieser grünen Linie. Sie schneiden die äußere Seite der beiden Parallelogramme auf der gleichen Höhe. Ebendiese Höhe entspricht auch der Höhe des neu anzubringenden Parallelogramms.
Schneidet man nun beiden Parallelogrammen entlang der grünen Linien die kleinen Dreiecke ab und fügt sie an der Spitze des gelben Dreiecks an, erkennt man, dass die Flächen der Bereiche gleicher Farbe übereinstimmen: Man schere die neu entstandenen Parallelogramme entlang der grünen Linie, bis beide auf der unteren Seite des Dreiecks "flachliegen", und verschiebe sie dann noch ein Stück abwärts, bis sie an der Seite hängen, statt auf ihr zu liegen.
Was gibt es, wenn man das Dreieck rechtwinklig macht und für die Parallelogramme speziell Quadrate wählt?
Den Kathetensatz und damit den pythagoreischen Satz, als deren Verallgemeinerung sich der Flächensatz von Pappos (von Alexandria, um 300 nach Christus, oft auch latinisiert Pappus geschrieben) erweist:
Schreiben Sie uns!
Beitrag schreiben