van Aubel

Beweisen Sie: Zeichnet man an die Seiten eines Vierecks Quadrate, so sind die Strecken vom Mittelpunkt eines Quadrats zu dem des gegenüberliegenden gleich lang und rechtwinkig zueinander.
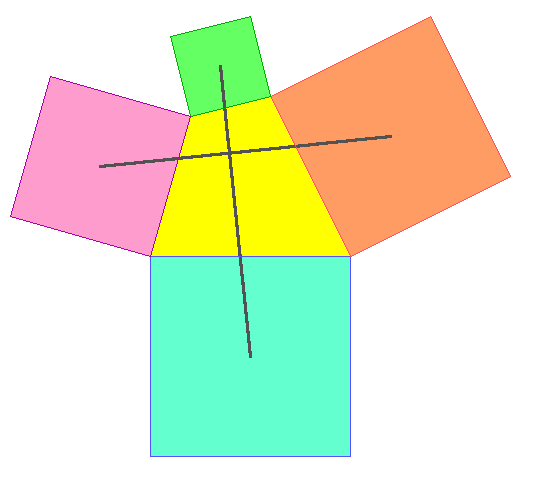
Zeichnen Sie Parallelen zu den halben Seiten des Vierecks und bilden Sie daraus durch Parallelverschiebung Polygonzüge.
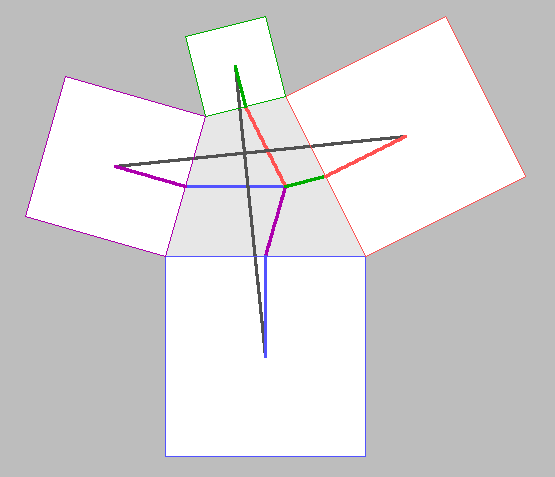
Die dick gezeichneten farbigen Linien waren, bevor sie an ihren aktuellen Platz verschoben wurden, halbe Seiten des jeweils gleichfarbigen Quadrats. Daraus entnimmt man, dass gleichfarbige dicke Linien jeweils gleich lang und zueinander rechtwinklig sind.
Wenn Sie den Sachverhalt lieber mit Symbolen durchdeklinieren wollen, können Sie Vektoren oder komplexe Zahlen nehmen oder kongruente Dreiecke bilden. Die Idee zu dem hier skizzierten Beweis habe ich dem Vektorbeweis im Ehrenwirth-Schulbuch "Anschauliche Analytische Geometrie" entnommen.Der Satz von Henricus Hubertus van Aubel (1830–1906) gilt auch für konkave oder überschlagene Vierecke, allerdings müssen die Quadrate immer nach rechts oder immer nach links angebaut werden, wenn man dem Umfang des Vierecks folgt. Das Viereck darf auch zu einem Dreieck oder sogar zu einer Strecke zusammenfallen.
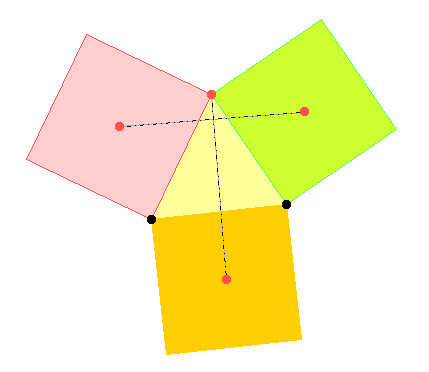
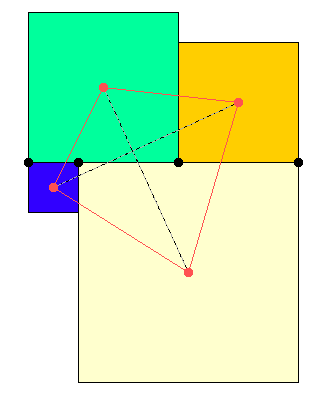
Für das Parallelogramm und für das rechtwinklige Dreieck wird es besonders einfach. Wo liegen die Ecken der vier Quadrate für das Parallelogramm?
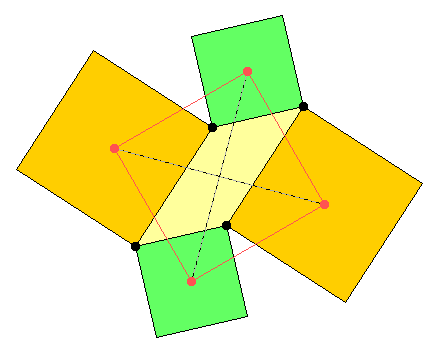
Die Symmetrie des Parallelogramms zieht nach sich, dass sich die beiden Strecken gegenseitig halbieren, und da sie – wie sonst auch – rechtwinklig zueinander liegen, sind sie die Diagonalen eines Quadrates.



Schreiben Sie uns!
Beitrag schreiben