Viele Rauten

Setzen Sie bitte in Gedanken (oder in Karton) auf die Seiten eines Dodekaeders Pyramiden, die gerade so hoch sind, dass ihre Dreiecke an den Kanten des Dodekaeders paarweise zu Rauten verschmelzen. Wie viele Ecken, Kanten und Rauten hat die entstehende Figur? Wie ist es, wenn Sie statt des Dodekaeders ein Ikosaeder nehmen?
An jeder Kante des Dodekaeders bzw. des Ikosaeders gibt es also eine Raute. Wo sind überall Ecken?
Die Ecken des Ausgangskörpers bleiben, aber dazu kommt über jeder Fläche eine zusätzliche. Das Rauten-Polyeder hat also so viele Ecken, wie das Ausgangspolyeder Ecken + Flächen hat, also in beiden Fällen 20 + 12 = 12 + 20 = 32; und es hat so viele Rauten, wie das Ausgangs-Polyeder Kanten hat, also auf jeden Fall 30. Ein Polyeder aus 30 Rauten heißt naheliegenderweise "Rhombentriakontaeder", und es hat 30 + 32 – 2 = 60 Kanten.
Dass das Ganze wunderschön aussieht, sehen Sie hier mit und ohne die Kanten des Ikosaeders und/oder des Dodekaeders:








Alle 30 Rauten sind deckungsgleich zueinander, aber die 32 Ecken sind von zweierlei Sorten: An den 12 Ecken des Ikosaeders, also "über" den 12 Flächen des Dodekaeders, gibt es Ecken, an denen sich je 5 Kanten des Triakontaeders treffen, und an den 20 Ecken des Dodekaeders, also "über" den 20 Flächen des Ikosaeders, treffen sich je 3 Kanten. Jede Raute hat je zwei Ecken von jeder der beiden Sorten, nämlich die beiden spitzen von der zuerst genannten und die beiden stumpfen von der anderen.
Polyeder mit nur einer Sorte deckungsgleicher (aber nichtregelmäßiger) Polygone und mehreren Sorten von Ecken sind nach Eugène Charles Catalan (1814–1894) benannt und gehören gemeinsam mit den archimedischen (eine Sorte Ecken, aber mehrere Sorten regelmäßiger Flächen) zu den halbregulären Polyedern. In jeder Raute des Rhombentriakontaeders wechseln sich die 4 Ecken wie 3 5 3 5 ab, diese Zahlenfolge charakterisiert es innerhalb der Catalan-Polyeder. Die gleiche Zahlenfolge 3535 kennzeichnet aber auch innerhalb der archimedischen Polyeder das Ikosidodekaeder, an dessen 30 Ecken sich jeweils 2 regelmäßige Dreiecke und Fünfecke entsprechend abwechseln. Es hat ebenfalls 60 Kanten, aber 32 Flächen, nämlich 20 Dreiecke (wie das Ikosaeder) und 12 Fünfecke (wie das Dodekaeder), es ist der gemeinsame Stumpf vom Ikosaeder und vom Dodekaeder, wenn man so viel abschneidet, dass von jeder der 30 Kanten (sowohl des Ikosaeders als auch des Dodekaeders) nur ein Punkt übrig bleibt. Ikosidodekaeder und Rhombentriakontaeder sind dual zueinander. Sie verhalten sich zu Ikosaeder und (Pentagon-)Dodekaeder wie Kuboktaeder und Rhombendodekaeder zum Oktaeder und zum Würfel.

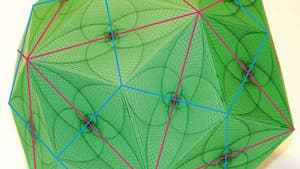
Während die Kanten des Ikosidodekaeders 6 ebene Zehnecke bilden, bestehen die des Rhombentriakontaeders aus 6 Gruppen zu je 10 Kanten, die rechtwinklig zu einer solchen Ebene und damit zueinander parallel sind. Hier tragen jeweils ein Zehneck und die zu ihm rechtwinkligen Triakontaederkanten dieselbe Farbe.
Kann man daraus eine Zerlegung des Triakontaeders in Rhombenhexaeder mit Kanten von genau diesen 6 Richtungen herleiten?
Das ist noch einmal das Rhombentriakontaeder mit Färbung der Kanten nach den 6 im Raum gleichmäßig verteilten Richtungen. Lässt man nun die 10 Kanten einer dieser Richtungen auf die Länge 0 schrumpfen, so verschwinden zugleich 10 Ecken und 10 Flächen, aber auch noch 10 weitere Kanten, denn es fallen 10-mal je zwei zusammen. Die 5-zählige Symmetrieachse, die parallel zu dieser Richtung ist, bleibt als einzige übrig. Wir bekommen das Rhombenikosaeder mit (nur noch) 20 Flächen, 22 Ecken und 40 Kanten.
Es ist aber durch die Zusammenziehung auch ein Volumen verschwunden, und zwar 10 Rhombenhexaeder, und zwar je 5 von der dünnen und 5 von der etwas dickeren Sorte. Es gibt nämlich zwei Möglichkeiten, aus den Rhomben mit dem goldenen Schnitt als Längenverhältnis der Diagonalen Hexaeder (verzerrte Würfel) zu bauen. Die dünnen haben 2 Ecken mit je drei stumpfen Rhomben-Ecken und 6 mit je zwei spitzen und einer stumpfen, die dicken haben umgekehrt zwei Ecken mit je drei spitzen und 6 mit je einer spitzen und zwei stumpfen. In dem verschwindenden Volumen bilden die 5 dicken die Mitte und die 5 dünnen einen Kranz außen herum.
Nun können wir auch im Rhomben-Ikosaeder parallele Kanten auf die Länge 0 schrumpfen lassen, und zwar genau 8 Stück. Dabei verschwinden 8 weitere Kanten, 8 Flächen und 8 Ecken, außerdem3 dicke und 3 dünne Hexaeder. Es bleibt also ein Rhombendodekaeder mit 12 Flächen, 24 Kanten und 14 Ecken. Das stimmt in den Anzahlen mit dem (von Kepler beschriebenen und) vom Würfel abstammenden halbregulären Catalan-Rhombendodekaeder überein, aber nicht in der Form. Das ergibt sich daraus, dass wir dort die Wurzel aus 2 als Diagonalenverhältnis in den Rhomben haben, hier aber den goldenen Schnitt (geerbt vom Triakontaeder): Es ist das Bilinksi-Rhombendodekaeder mit 2 Ecken mit je 4 spitzen Rhombenecken, 4 Ecken mit 3 stumpfen, 4 mit 3 spitzen und einer stumpfen und 4 mit einer spitzen und 2 stumpfen. Zum Vergleich: Das kubische Rhombendodekaeder hat 6 Ecken mit 4 spitzen und 8 mit je 3 stumpfen.
Das Bilinski-Rhombendodekaeder kann man – wie in der Animation gezeigt – in 2 dicke und 2 dünne Hexaeder teilen. Die Aufteilung der Volumina erlaubt natürlich verschiedene Anordnungen und gibt daher Anlass zu einem schönen Puzzle-Spiel aus 10 dicken und 10 dünnen "goldenen" Rhombenhexaedern.
Die Zahlen der Ecken usw. fassen wir in dieser Tabelle zusammen:
| Polyeder: | Rh.-Hexaeder | Rh.-Dodek. | Rh.-Ikos. | Rh.-Triak. |
| Ecken (außen): | 8 | 14 | 22 | 32 |
| Kanten (außen): | 12 | 24 | 40 | 60 |
| Rhomben (außen): | 6 | 12 | 20 | 30 |
| dicke u. dünne Hex.: | 1 | 2 + 2 | 5 + 5 | 10 + 10 |
Alle diese Rhomboeder benutzen für ihre Kanten bis zu 6 Richtungen, alle diese 6 verteilen sich im Raum gleichmäßig. Wenn man nur 3 Richtungen nimmt und sie gleichmäßig verteilt, kommt man zum Würfel als dem regulären Rhombenhexaeder, nimmt man aber 3 (oder 4 oder 5) von unseren 6 Richtungen, so bewahren wir den goldenen Schnitt als Diagonalenverhältnis der Rhomben. Bei 3 Richtungen bekommen wir das dicke und das dünne Rhombenhexaeder, bei 4, 5 oder allen 6 können wir die Polyeder aus genau solchen zusammensetzen, und zwar gleich vielen dicken und dünnen.
\(n\) ist im Folgenden eine der Zahlen 3 bis 6. Wenn wir \(n\) der 6 Richtungen benutzen, spannen wir \(n(n-1)/2\) Flächen-Richtungen auf (jede mit jeder anderen, wegen Doppelzählung durch 2 zu teilen). Die Außenflächen (Rhomben) liegen paarweise in diesen Flächen-Richtungen, es gibt also \(n\cdot(n-1)\) von ihnen (vergleichen Sie diese Ergebnisse mit den Zahlen der Tabelle!).
Da alle (Außen-)Flächen Rhomben und somit Vierecke sind, hat das Polyeder doppelt so viele Kanten wie Flächen, also \(2n\cdot(n-1)\) Kanten. Da die Euler-Charakteristik (Zahl der Flächen + die der Ecken – die der Kanten) = 2 ist (wie für konvexe Polyeder allgemein zutreffend), bekommen wir für die Zahl der Ecken \(n(n-1)+2\), also z. B. 32 für das Triakontaeder.
Aus dem Bisherigen folgt sogleich, wie sich die Volumina von Rhomben-Dodekaeder, -Ikosaeder und -Triakontaeder zueinander verhalten: nämlich wie 2:5:10.



Schreiben Sie uns!
Beitrag schreiben