Hemmes mathematische Rätsel: Vier Schnecken
Leo Moser wurde 11. April 1921 in Wien geboren und emigrierte schon als Kind im Alter von drei Jahren mit seinen Eltern nach Kanada. Er studierte dort Mathematik und hatte seit 1951 eine Professur an der Universität von Alberta. Moser kannte sich in vielen Gebieten der Mathematik hervorragend aus, veröffentlichte über hundert wissenschaftliche Arbeiten und galt als einer der besten Lehrer, welche die Universität von Alberta jemals hatte. Er war ein ausgezeichneter Schachspieler, Magier und Erfinder von Denksportaufgaben. Leo Moser starb am 9. Februar 1970 im Alter von nur 48 Jahren. 1951 veröffentlichte er im Januar-Februar-Heft der Zeitschrift Mathematics Magazine ein hübsches Rätsel über spiralförmige Wege.
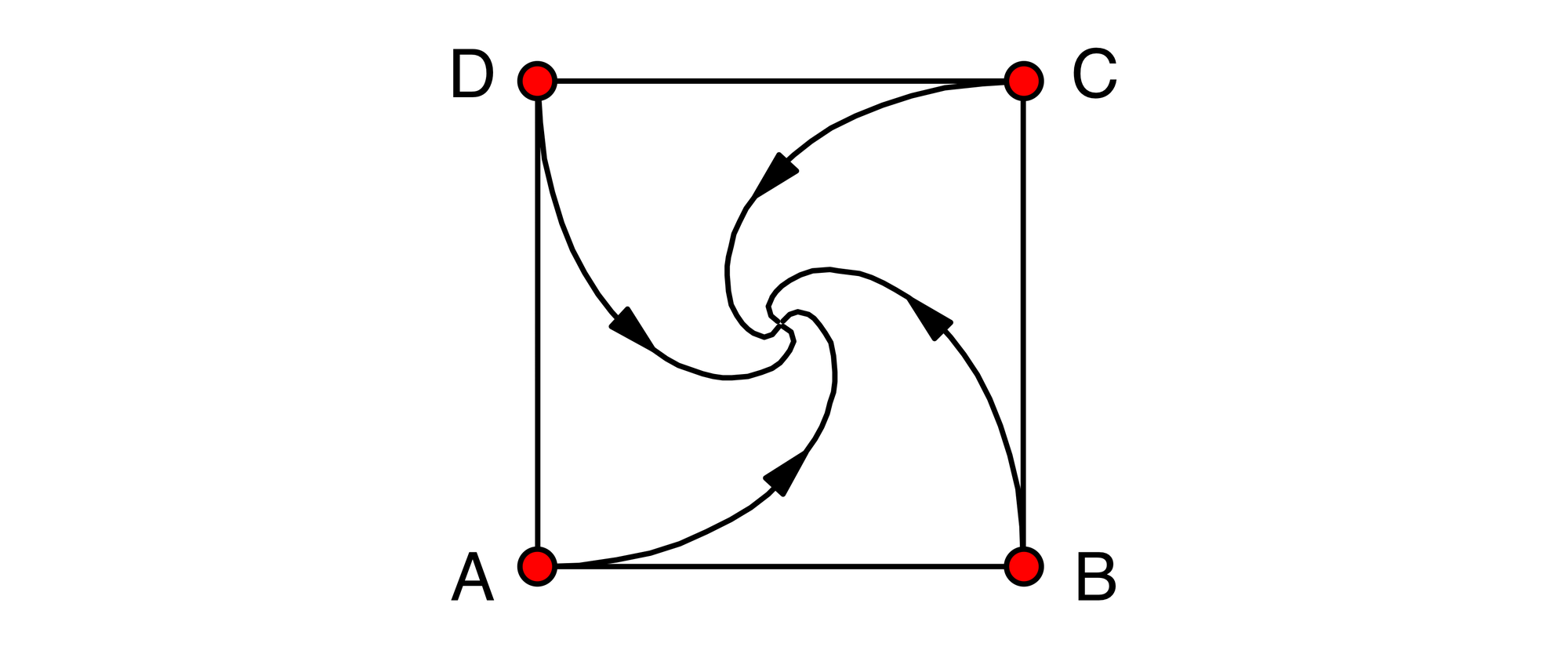
Vier Schnecken − Adele, Berta, Carla und Dora − sitzen auf den Ecken eines Quadrates von einem Meter Seitenlänge. Gleichzeitig und mit gleichen Geschwindigkeiten kriechen Adele auf Berta, Berta auf Carla, Carla auf Dora und Dora auf Adela zu. Da die Schnecken ständig ihre Richtungen ändern müssen, um immer genau aufeinander zu zu kriechen, sind ihre Bahnen Spiralen, die sich im Mittelpunkt des Quadrates treffen. Wie lang ist der Weg jeder Schnecke bis zum Treffpunkt?
Zu jedem Zeitpunkt bilden die vier Schnecken die Eckpunkte eines Quadrats, das ständig schrumpft und gleichzeitig um seinen Mittelpunkt rotiert. Der Weg jeder Schnecke steht daher immer senkrecht auf dem Weg der Schnecke, auf die sie zu kriecht. Das bedeutet, dass bei Annäherung von Adele an Berta keine Komponente in der Bewegung von Berta auftritt, die Berta auf Adele zu oder von Adele weg führt.
Folglich vermindert sich der Abstand von Adele zu Berta genau um den von Adele zurückgelegten Weg, und Adele wird mit Berta zum gleichen Zeitpunkt zusammentreffen, als wenn Berta sich gar nicht bewegt hätte. Die Länge jedes Weges ist also gleich der Seitenlänge des Quadrats: ein Meter.
Die Bahnkurven, die die Schnecken kriechen, sind übrigens logarithmische Spiralen. Sie haben ganz allgemein die Form r(a) = r0ekα. Dabei ist r der Abstand eines Bahnpunktes vom Zentrum der Spirale und α der Winkel, den der Radius eines Bahnpunktes ab dem Radius r0 überstreicht. Die Größe k ist eine Konstante. In diesem konkreten Fall der vier Schnecken beträgt r0 = 1 m ⁄ √2 und k = −1.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.