Hemmes mathematische Rätsel: Welcher Körper passt in alle drei Öffnungen?
1780 gründete Peter Friedrich Catel in Berlin einen Versandhandel für mathematisches und physikalisches Spielzeug. Dort tauchte erstmals in der Denksportliteratur das bekannte Problem der drei mathematischen Löcher auf.
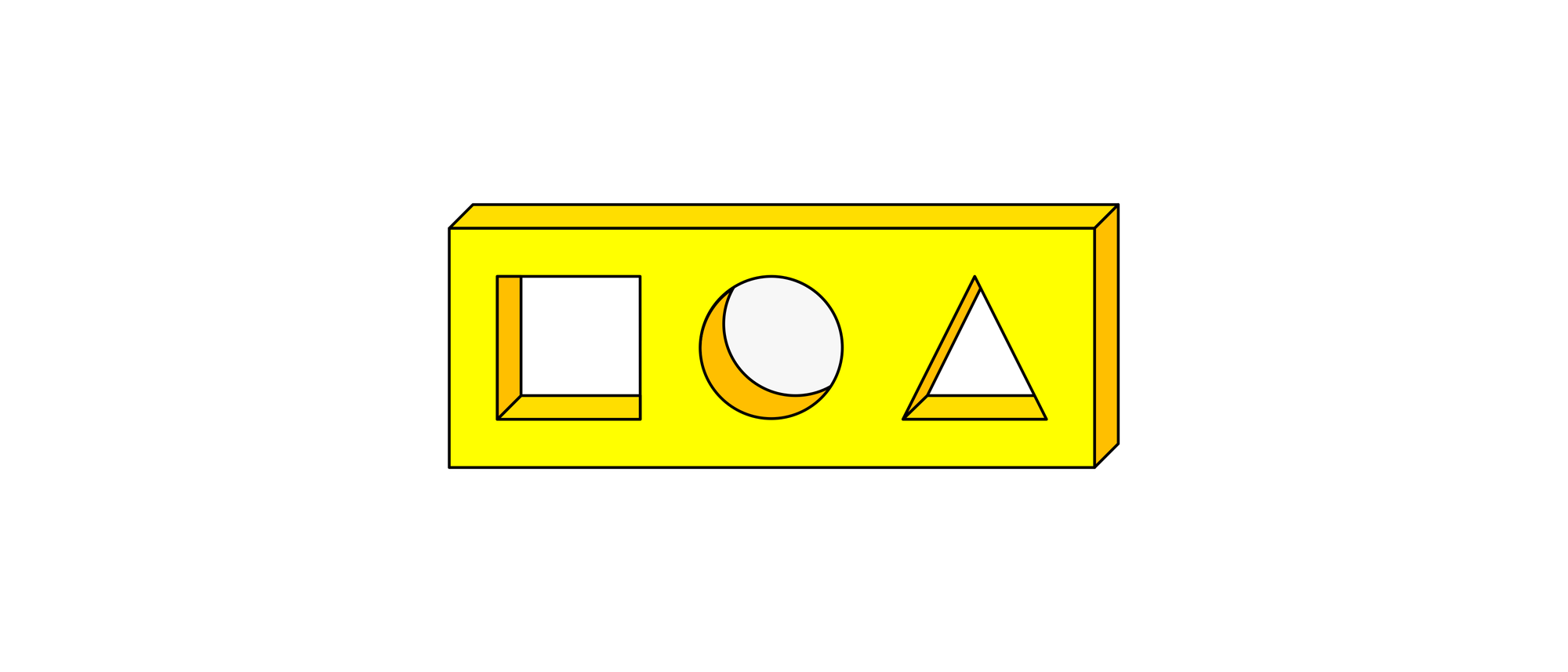
Gibt es einen Körper, den man konturengleich nacheinander durch alle drei Löcher des Brettchens stecken kann?
Konturengleich bedeutet, dass sich mit dem Körper die Öffnungen vollständig verschließen lassen, so dass man an keiner Stelle mehr hindurchsehen kann. Die Seiten des quadratischen Lochs, der Durchmesser des runden Lochs und die Grundseite und die Höhe des dreieckigen Lochs sind alle gleich lang.
Es gibt mehrere Körper, die sich konturengleich durch die drei Löcher stecken lassen.
Die einfachste Form erhält man, indem man einen geraden Kreiszylinder nimmt, dessen Durchmesser und Höhe gleich sind, und davon dann durch zwei ebene Schnitte zwei gleiche Stücke so entfernt, wie es die Zeichnung dargestellt ist.
Nun ist die Kontur in der Draufsicht ein Kreis, in der Seitenansicht ein gleichschenkliges Dreieck und in der Vorderansicht ein Quadrat.

Schreiben Sie uns!
Beitrag schreiben