Knotentheorie: Die Mathematik des Strickens

So mancher sucht derzeit ein neues Hobby. Wie wäre es mit Stricken? Die Physikerin Elisabetta Matsumoto vom Georgia Institute of Technology kann das nur empfehlen. Sie strickt seit ihrer Kindheit leidenschaftlich gern und besitzt zahlreiche Bücher mit verschiedenen Anleitungen, um mit einem Wollfaden und zwei Stricknadeln vielseitige Muster aus einzelnen Maschen zu bilden.
Als Naturwissenschaftlerin begann Matsumoto irgendwann, etwas genauer über ihr Hobby nachzudenken. Denn kleine, kaum sichtbare Veränderungen im Strickmuster können das Endergebnis stark beeinflussen. Verwendet man beispielsweise nur eine einzige Art von Masche, rollt sich der Stoff an den Rändern auf. Kombiniert man hingegen zwei verschiedene Maschenarten miteinander, ist das entstandene Gewebe völlig eben.
Doch auch die mechanischen Eigenschaften eines Stoffs hängen erheblich vom Strickmuster ab: Manche Stoffe sind elastisch, während andere steif sind und sich kaum auseinanderziehen lassen. Tatsächlich zählen Strickwaren zu äußerst ungewöhnlichen Materialien: Sie bestehen aus einem nicht dehnbaren Faden, sind aber als Gesamtes elastisch.
Ein beeindruckender Drache
Das Interesse der Physikerin war endgültig geweckt, als sie den »Dragon of Happiness« von Sharon Winsauer entdeckte. Dabei handelt es sich um ein Tuch, dessen Mitte ein imposanter Drache ziert. Von diesem Motiv verzaubert, machte sich Matsumoto ans Werk und strickte die komplizierte Struktur nach: »Ich habe Bücher mit Tausenden von verschiedenen Strickmustern«, sagt sie im Gespräch mit der Wissenschaftsseite »ScienceNews«. »Aber den ›Dragon of Happiness‹ hatte ich noch nie gesehen.« Die Maschen nehmen dabei nicht nur eine einzige Zelle des Musters ein, sondern erstrecken sich über weite Bereiche und scheinen eher einer horizontalen als der üblichen vertikalen Ausrichtung zu folgen.
All diese Mechanismen zu verstehen, setzte sich Matsumoto vor einigen Jahren zum Ziel. Sie beschloss, eine Theorie des Strickens zu entwickeln, um die verschiedenen Maschen zu kategorisieren und deren Kombinationen zu charakterisieren: Wie elastisch ist ein Stoff, wenn man ihn aus diesen und jenen Maschen aufbaut? Gemeinsam mit ihrem Doktoranden Shashank G. Markande wandte sie sich der Knotentheorie zu, um die Kunst des Strickens wissenschaftlich zu untersuchen.
Strickwaren bestehen aus aneinandergereihten Fadenschlingen, die ein Gitter bilden. Es gibt zwei grundlegende Maschen (rechte und linke), aus denen sich allerlei Muster erzeugen lassen. Um herauszufinden, wie sich der so hergestellte Stoff verhält, muss man die Eigenschaften der einzelnen Schlingen sowie die Reihenfolge, in der sie auftreten, verstehen.
Die Wissenschaft von Knoten
Diese Aufgabe fällt in den Bereich der Knotentheorie, einer Disziplin, die sich der Mathematik von Schlingen widmet. Anders als das, was man im Alltag als Knoten bezeichnet – zum Beispiel die Schlaufe in den Schnürsenkeln –, bezieht sich der Begriff in der Mathematik ausschließlich auf geschlossene Strukturen ohne lose Enden. Damit ist jedes Strickmuster aus Sicht der Knotentheorie uninteressant, denn zieht man an einem Faden eines Strickmusters, löst man die Schlingen auf und zerstört das Gewebe.
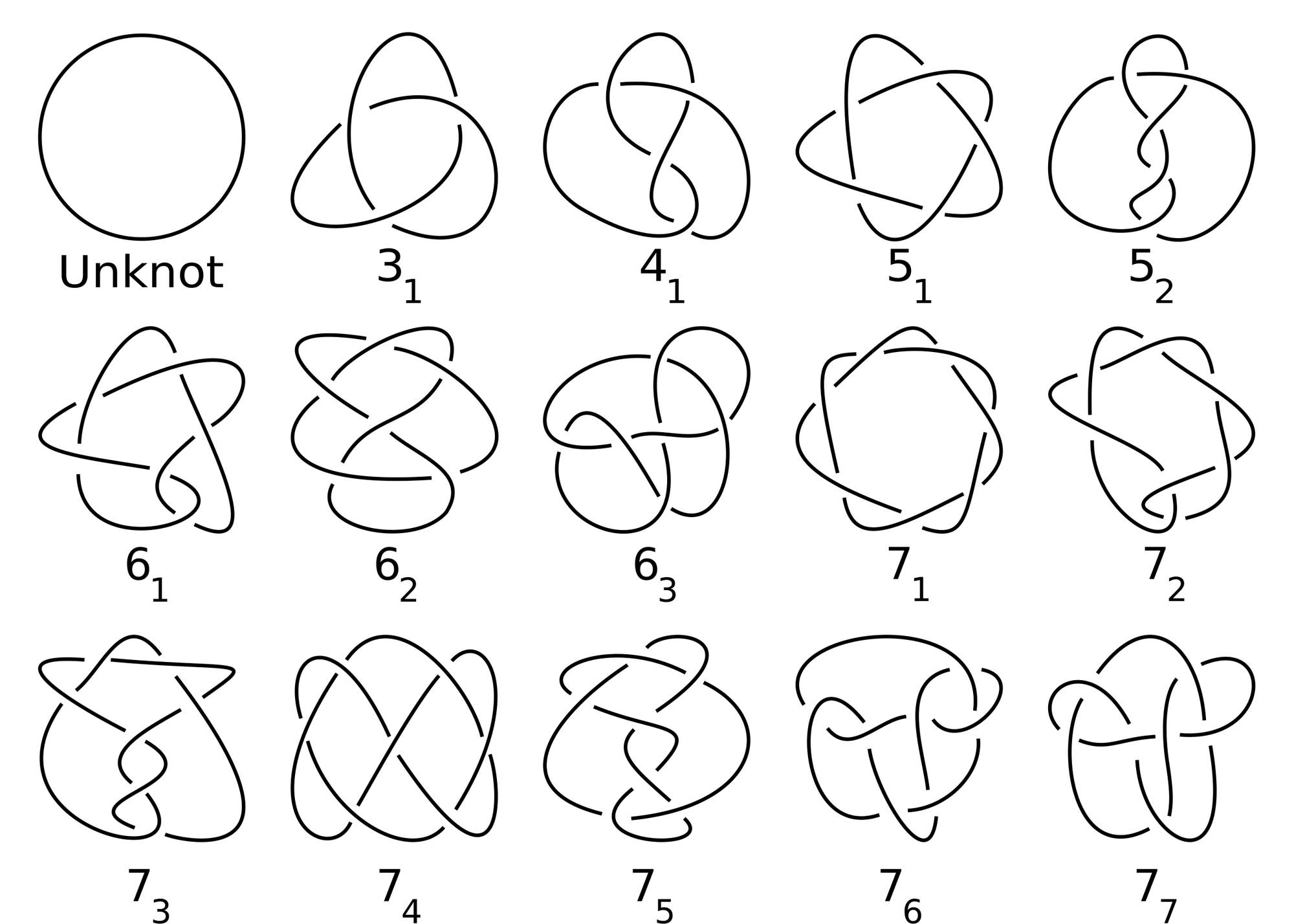
Daher behalfen sich Matsumoto und Markande mit einem Trick: Sie betrachteten einen Stoff als doppelt periodisch, das heißt, das obere Ende geht in das untere über, genauso wie das linke in das rechte Ende. Es ist, als würde man einen Schal stricken und irgendwann dessen Anfang nahtlos mit dem Ende zusammenfügen und die zwei seitlichen Ränder ebenfalls. Die dadurch entstehende Figur ist ein Donut, Mathematiker nennen sie Torus. Folgt man dem Faden auf diesem Torus, so bildet dieser mit all seinen Windungen und Schlingen einen komplizierten Knoten – und zwar im strengen mathematischen Sinn, denn er hat weder Anfang noch Ende.
Indem die Physikerin und der Physiker Strickmuster auf diese Weise betrachten, können sie Methoden aus der Knotentheorie nutzen, um den Schlingen ihre Geheimnisse zu entlocken. Mathematiker untersuchen hier unter anderem, welche Knoten äquivalent sind und welche sich grundlegend voneinander unterscheiden. Auch wenn es überraschend scheint, ist das nämlich nicht immer einfach. Stellen Sie sich vor, vor Ihnen liegt ein Blatt Papier mit zwei darauf abgebildeten, komplizierten Knoten. Können Sie auf den ersten Blick beurteilen, ob sie gleich sind? Vielleicht wurden sie ja bloß aus einem anderen Winkel abgebildet und sehen deshalb zunächst verschieden aus.
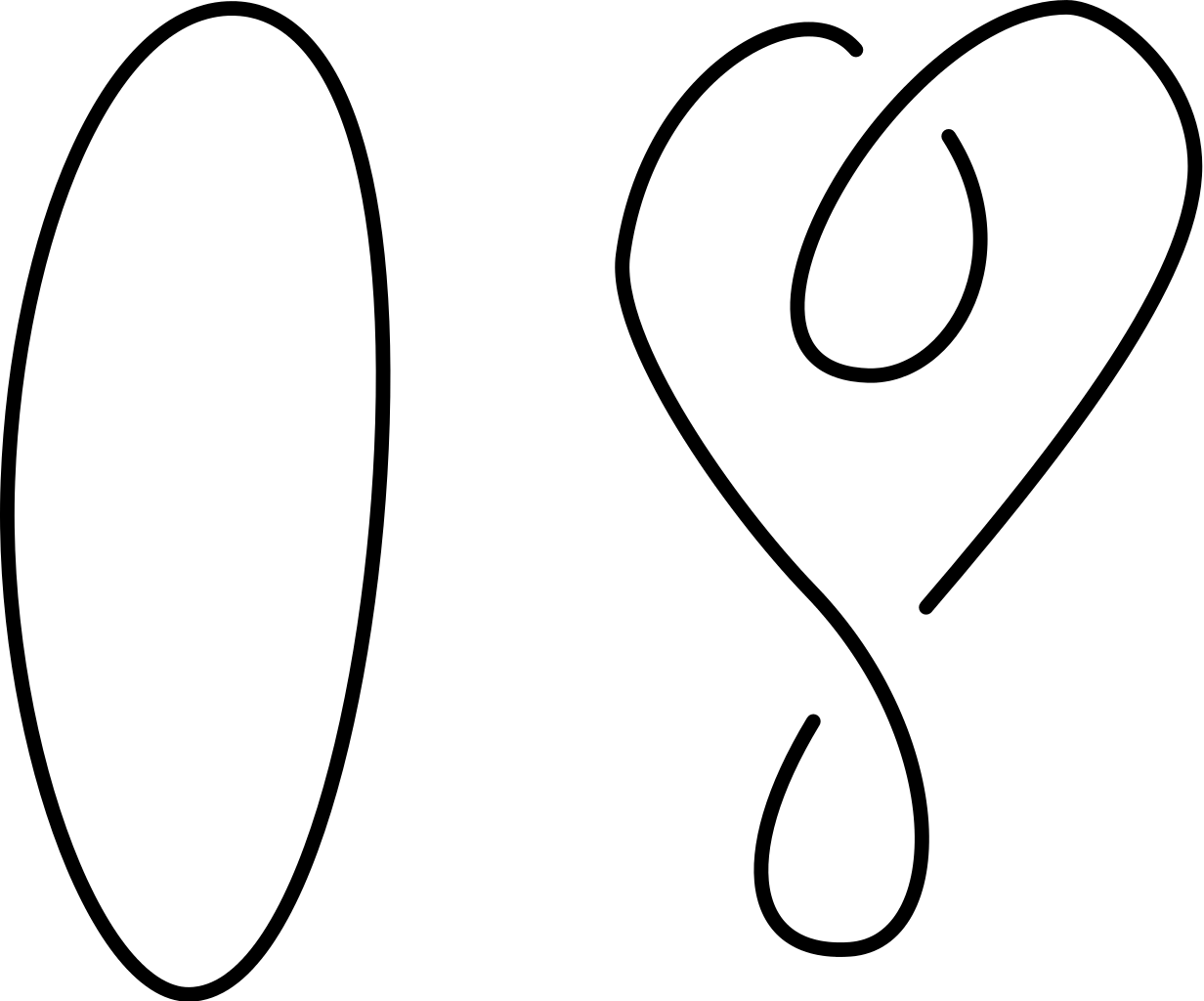
Diese Aufgabe beschäftigt Knotentheoretiker schon seit Jahrhunderten – doch eine vollständige Lösung haben sie bis heute nicht. Um komplizierte Objekte zu kategorisieren, nutzen Mathematiker gerne so genannte Invarianten. Dabei handelt es sich um Größen, die sich aus fundamentalen Eigenschaften der betreffenden Objekte berechnen lassen, etwa der Anzahl von Löchern in einer Oberfläche. Invarianten bleiben gleich, wenn man die Figuren leicht verändert, sie etwa in die Länge zieht oder zusammenstaucht.
Auch zweidimensionalen Abbildungen von Knoten kann man allerlei Invarianten zuordnen. Sind die Knoten gleich, müssen sie über dieselben Invarianten verfügen. Doch leider gilt der Umkehrschluss nicht. Stimmen die Invarianten überein, heißt das nicht, dass die Schlingen zwangsweise äquivalent sind.
Computer als Hilfsmittel
Dennoch gibt es inzwischen Computerprogramme, die zweidimensionale Abbildungen von Knoten untersuchen und vergleichen, um deren Eigenschaften preiszugeben. Matsumoto und Markande wollten deshalb eine Methode finden, mit der jedes mögliche Strickmuster systematisch durch eine zweidimensionale Abbildung darstellbar ist, die ein Computer analysieren kann.
Das ist ihnen nun gelungen. In einer kürzlich erschienenen Arbeit, die sie im August 2020 auf der »Bridges«-Konferenz vorstellten, beschreiben sie, wie man aus einer Mischung von Halbkreisen und Geraden auf der Geometrie eines Torus jedes mögliche Strickmuster aus verschiedenen Maschen darstellen kann. Allerdings weisen sie darauf hin, dass nicht jedes derart erzeugte Muster auch tatsächlich realisierbar ist: Es ist möglich, Verschlingungen zu konzipieren, die sich nicht mit zwei Stricknadeln und einem Faden umsetzen lassen.
Inzwischen bringen Matsumoto und ihre Kollegen einem Computer das Stricken bei. Sie füttern die Maschine mit Garneigenschaften, mathematischen Details der Maschen und den gewünschten Mustern. Anschließend berechnet ein Algorithmus die mechanischen Eigenschaften des dadurch entstehenden Stoffs. Das könnte dabei helfen, Materialien für bestimmte Anwendungen maßzuschneidern – und vielleicht knifflige Alltagsprobleme zu lösen.





Schreiben Sie uns!
Beitrag schreiben