Vorweg einige heuristische Betrachtungen: Beim gleichseitigen Dreieck ist das Verhältnis jeder Schwerlinie (hier zugleich Höhe und Mittellot und Winkelhalbierende) zu jeder Seitenlänge gleich \(\sqrt{3/4}\).

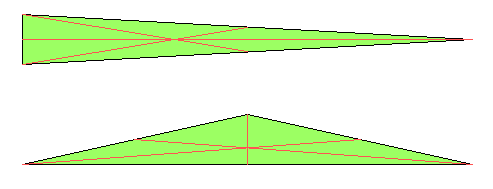
Das gleichschenklige Dreieck bietet zwei (wie wir sehen werden: extreme) Grenzfälle: Ist es ganz steil (also mit verschwindend kleiner Grundseite), so erreichen die Schwerlinien zusammen fast den Umfang. Ist es dagegen extrem flach (Grundseite fast die doppelte Schenkellänge), so ist die Summe der Schwerlinien fast nur 3/4 des Umfangs.

In diesen Bildern muss man sich die (vertikal gezeichnete) Höhe gegen 0 schrumpfend vorstellen:

Dass tatsächlich alle Dreiecke zwischen diesen Extremfällen liegen, sehen wir so (Coxeter Aufgabe 2 in 1.4):

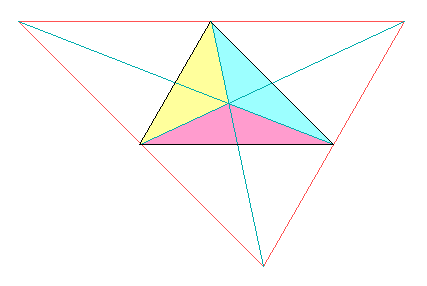
Das Bild zeigt ein Dreieck und in Drehstreckung mit Verdopplung und halber Drehung seine Vergrößerung, sowie darin alle Schwerlinien, die sich bekanntlich gegenseitig im Verhältnis (1/3):(2/3) teilen.

Wir wenden die Dreiecksungleichung zuerst auf die drei getönten Teildreiecke an: Jede Seite des urspünglichen Dreiecks ist kürzer als die Summe von je 2/3 der Längen der nicht zu ihr gehörenden Schwerlinien. Bilden wir für alle drei die Summe, so ist der Umfang (Summe der Seitenlängen) kleiner als 4/3 der Summe der Schwerlinien, diese also größer als 3/4 des Umfangs.

Nun wenden wir die Ungleichung auf die in den folgenden drei Bildern getönten Dreiecke an, die jeweils aus zwei verschiedenen Seiten des Orginal-Dreiecks und dem Doppelten einer Schwerlinie gebildet werden. Bilden wir auch hier die Summen über die drei zyklischen Vertauschungen, so finden wir, dass die Seiten zusammen länger als die Schwerlinien zusammen sind.

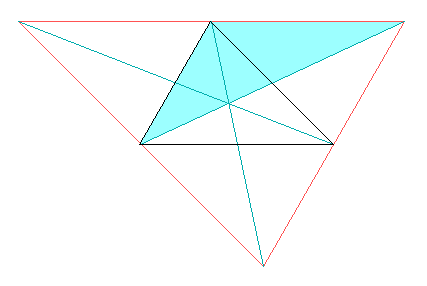
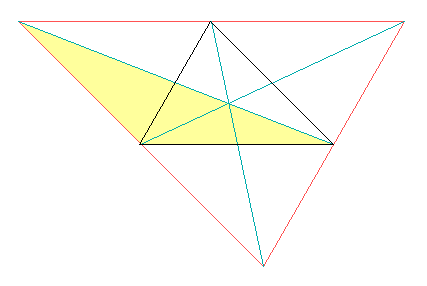
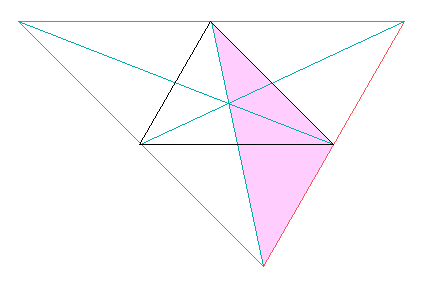
Die Summe der Schwerlinien ist also größer als 3/4 des Umfangs und kleiner als der ganze Umfang.