Hemmes mathematische Rätsel: Wie muss man das E zerschneiden?
Henry Ernest Dudeney (1857–1930) war wohl der bedeutendste Rätselerfinder, der jemals lebte. 1926 veröffentlichte er im »Strand Magazine« das folgende Zerlegungsproblem.
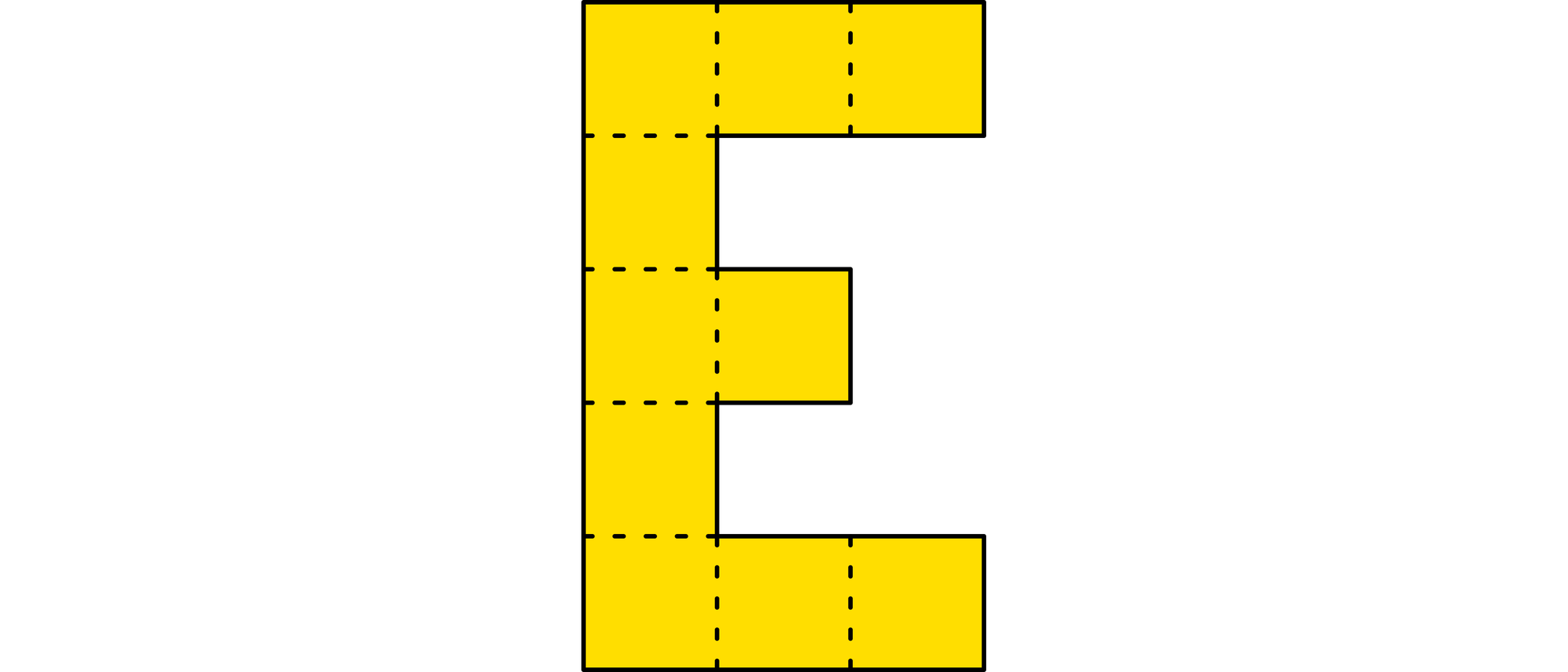
Das E setzt sich auch zehn gleichen Quadraten zusammen. Zerschneiden Sie das E in möglichst wenige Teile, so dass Sie diese anschließend zu einem Quadrat zusammensetzen können.
Die Teile dürfen dabei umgeklappt werden, sodass die Unter- zur Oberseite wird. Es müssen alle Teile für das Quadrat verwendet werden. In dem Quadrat darf es keine Lücken und keine Überlappungen geben.
Da das E und somit auch das daraus entstehende Quadrat Flächen von 10 Quadrateinheiten haben, müssen die Seiten des Quadrates √10 Einheiten lang sein. Eine Diagonale durch ein Rechteck, das aus drei nebeneinanderliegenden Quadraten besteht, hat genau diese Länge. Darum ist es möglich, dass man die vier Quadratseiten durch Diagonalschnitte durch zwei Quadrattripel erreichen kann.
Legt man die beiden Diagonalschnitte so durch den oberen und den unteren Balken des E, wie es die Abbildung zeigt, braucht man nur noch den senkrechten Balken direkt unter dem mittleren Querbalken durchzuschneiden, um die so entstandenen vier Stücke zu einem Quadrat zusammensetzen zu können. Mit weniger Teilen gelingt es jedoch nicht.
Schreiben Sie uns!
Beitrag schreiben