Mit dem Abwurf der Atombomben auf Hiroshima und Nagasaki im Jahr 1945 veränderten die USA die Art der Kriegsführung. Bald darauf begannen auch andere Länder an der neuen Waffentechnologie zu forschen, allen voran die Sowjetunion. Die ersten Kernwaffentests fanden meist in abgelegenen Gebieten der USA, Zentralasiens oder in Überseegebieten statt. Die Explosionen waren für die ganze Welt sichtbar – und das sollten sie auch, handelte es sich doch vorwiegend um eine Machtdemonstration.

In den 1950er Jahren nahm die Zahl der Tests rasant zu – mit schwer wiegenden Folgen: Die Radioaktivität in der Erdatmosphäre stieg Besorgnis erregend schnell an.

Daher begannen die USA und die Sowjetunion, über mögliche Einschränkungen der Kernwaffentests zu verhandeln. Eine Einigung ergibt aber natürlich nur dann Sinn, wenn man sicherstellen kann, dass sich beide Parteien daran halten. Während Detonationen an der Oberfläche, im All oder Unterwasser relativ leicht zu detektieren sind, sieht das im Untergrund völlig anders aus. Wie lässt sich herausfinden, ob ein anderes Land keine Kernwaffen tief unter der Erde sprengt, wenn man keinen Zugang zu dort befindlichen Seismometern hat? Lassen sich die Explosionen von gewöhnlichen Erdbeben unterscheiden?

1963 einigten sich die USA, Großbritannien und die Sowjetunion darauf, keine Kernwaffenversuche in der Atmosphäre, im Weltraum und unter Wasser mehr durchzuführen. Im Untergrund war hingegen alles erlaubt – kontrollieren konnte es sowieso niemand. Das änderte sich allerdings 1965: Damals wurde ein Algorithmus veröffentlicht, der es ermöglicht, gewöhnliche Erdbeben von Explosionen zu unterscheiden. Wäre er ein paar Jahre früher entwickelt worden, hätte man vielleicht auch unterirdische Atomwaffentests in die Verbotsliste aufnehmen können. Damit hätte es für die Unterzeichner keine Möglichkeit mehr gegeben, die Bomben zu testen. »Es hätte definitiv geholfen«, sagt der Physiker Richard Garwin, einer der damaligen politischen Berater auf die Frage, ob ein früheres Erscheinen zu einer Welt ohne Kernwaffen beigetragen hätte. »Das hätte das Blatt durchaus wenden können.«

Garwin war in den 1960er Jahren Mitglied des Science Advisory Committee, eines Ausschusses von Wissenschaftlern, die den US-Präsidenten berieten. Der Physiker hatte sich dort seinen Platz gesichert, da er in den 1950er Jahren die theoretischen Grundlagen für die Wasserstoffbombe gelegt hatte. Zeitgleich war auch der Mathematiker John Tukey Teil des Komitees. »Ich saß gerne neben Tukey, weil er immer eine Packung getrockneter Pflaumen dabei hatte«, erzählt Garwin in einem Interview mit dem Journalisten Dan Ford. In einer der Sitzungen ertappte der Physiker seinen Kollegen Tukey dabei, wie er komplizierte Berechnungen auf seinen Block kritzelte. Garwin erkannte, dass es sich um Fourier-Transformationen handelte, eine mathematische Konstruktion, die in unzähligen Bereichen Anwendung findet – von der Bild- und Tonverarbeitung über die Berechnung von Polynomen die Analyse von Kristallstrukturen bis hin zur Verarbeitung seismologischer Signale. Wie sich herausstellte, waren Tukeys Kritzeleien der Schlüssel, um gewöhnliche Erdbeben von unterirdischen Kernwaffentests zu unterscheiden.

Der Unterschied zwischen Erdbeben und Kernwaffentests

Jede Erschütterung hat einzigartige charakteristische Merkmale. Da Erdbeben und unterirdische Explosionen verschiedene Ursachen haben, sind deren seismische Signale zwangsläufig unterschiedlich. Erdbeben haben oft ein spezielles Muster: Zuerst breiten sich Primärwellen aus, die in Ausbreitungsrichtung schwingen, dann folgen die langsameren Scherwellen, die quer zur Ausbreitungsrichtung oszillieren. Bei Explosionen gibt es diese beiden Wellenformen ebenfalls, doch die Primärwellen fallen in diesem Fall bei manchen Frequenzen deutlich stärker aus.

Um ein seismisches Signal analysieren zu können, muss man es in seine Grundbestandteile zerlegen: in eine Überlagerung aus Wellen verschiedener Frequenzen. Das Ganze kennt man aus der Musik, wenn man einen Klang in seine Obertöne zerlegt.

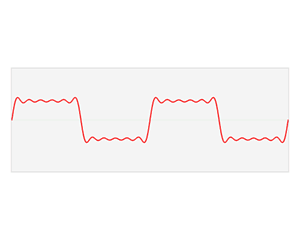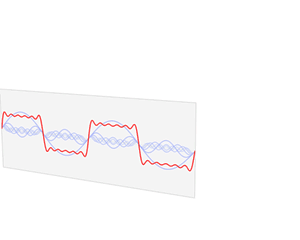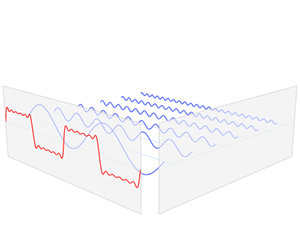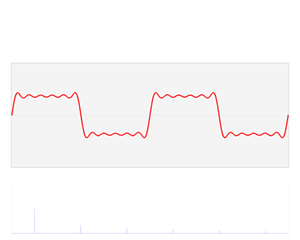
Praktisch bedeutet das: Man sucht jene Sinus- und Cosinusfunktionen, die addiert das zu untersuchende Signal ergeben. Wenn man beispielsweise wissen möchte, ob die Sinuskurve sin(fx) einer bestimmten Frequenz f zum Signal beiträgt, kann man das Signal (beziehungsweise die Datenpunkte, die man aufgenommen hat) mit der Sinusfunktion sin(fx) multiplizieren und dann ermitteln, welche Fläche das Ergebnis mit der x-Achse einschließt.

Da die Sinusfunktion gleich viele Anteile hat, die oberhalb und unterhalb der x-Achse verlaufen, enthält ihr Produkt mit dem Eingangssignal nur dann eine nicht verschwindende Fläche, wenn beide auf irgendeine Weise zusammenhängen. Wenn die Sinusfunktion und das Signal hingegen nicht korreliert sind, dann hat ihr Produkt (über den ganzen Raum betrachtet) genauso viele positive wie negative Anteile, so dass die mit der x-Achse eingeschlossene Fläche verschwindet. Das heißt: Ist die addierte Fläche null, dann ist die betrachtete Sinusfunktion nicht Teil des Signals. Andernfalls gibt die Größe der Fläche an, wie stark die Sinuswelle mit dieser Frequenz zum Signal beiträgt. Gleiches gilt natürlich auch für den Cosinus. Um ein Signal zu charakterisieren, muss man es also für alle f mit sin(fx) und cos(fx) multiplizieren und dann die jeweils eingeschlossenen Flächen berechnen. Das Signal S lässt sich dann schreiben als: S ≈ Σ_f (A_fsin(fx) + B_fcos(fx)), wobei die Vorfaktoren A_f und B_f von den zuvor berechneten Flächen abhängen.

Durch diese Zerlegung in Sinus- und Cosinusfunktionen lässt sich bestimmen, ob eine seismische Erschütterung von einem Erdbeben oder einer Explosion verursacht wurde. Die mathematischen Grundlagen für diese so genannte Fourier-Analyse sind seit Beginn des 19. Jahrhunderts bekannt. Allerdings ist das Verfahren nicht immer einfach umzusetzen.

Die erste Schwierigkeit besteht darin, dass ein aufgezeichnetes Signal keine kontinuierliche Kurve ist, sondern aus diskreten Datenpunkten besteht. Je größer der Abstand zwischen den Datenpunkten, desto ungewisser ist, ob hochfrequente Signale Teil der Kurve sind. Ein zweites Problem ist, dass die Aufzeichnung nicht unendlich lang ist, sondern meist nur über eine kurze Zeit erfolgt. Dadurch lässt sich nicht beurteilen, welche von zwei nah beieinander liegenden Frequenzen wirklich im Signal enthalten ist – das Frequenzspektrum wird dadurch unscharf. Die niedrigste Frequenz f_min, die man sinnvoll auflösen kann, ist jene, deren Periode der Länge L des gesamten Signals entspricht. Die Kurven, die dieser Frequenz entsprechen, sind durch sin(2πx/L) und cos(2πx/L) gegeben. Wenn man nun N Datenpunkte im gleichen Abstand untersuchen möchte, beginnt man mit den Kurven der niedrigsten Frequenz und arbeitet sich dann zu ganzzahligen Vielfachen n der Frequenz vor: n·f_min. Das entspricht den Funktionen sin(2·2πx/L), sin(3·2πx/L), sin(4·2πx/L), …, sin(N·2πx/L) (Gleiches natürlich für den Cosinus). Es ist nicht sinnvoll, höhere Frequenzen als N·f_min zu untersuchen, da die Periode der zugehörigen Funktionen kürzer ist als der Abstand benachbarter Datenpunkte. Alles darüber hinaus übersteigt unser Auflösungsvermögen.

Um die Fourier-Analyse mit diskreten Messwerten durchzuführen, multipliziert man also jeden der N Datenpunkte mit N verschiedenen Sinus- und Cosinusfunktionen und ermittelt daraus die mit der x-Achse eingeschlossene Fläche. Ein Computer muss also N² Rechenschritte durchführen. Das stellt für große Datenmengen ein Problem dar: Während man ein Signal aus acht Datenpunkten im Handumdrehen in seine Bestandteile zerlegen kann, ist das mit einer Million Datenpunkte schon schwieriger, denn dafür sind 10¹² Rechenschritte nötig. Ein moderner Rechner mit 3,5 Gigahertz bräuchte dafür unter Volllast etwa fünf Minuten. Für Computer in den 1960er Jahren war diese Aufgabe unlösbar. Möchte man 100-mal so viele Datenpunkte analysieren, wächst die Anzahl der Rechenschritte um den Faktor 10 000 an – damit wären auch unsere Rechner heillos überfordert.

Hier kommen Tukeys Kritzeleien ins Spiel. Er hatte damals eine Idee formuliert, wie sich die Fourier-Transformation schneller umsetzen lässt. Aus N² Rechenschritten werden durch seine Methode nur noch N·log₂N. Das klingt zwar nur nach einer kleinen Verbesserung, doch bei vielen Datenpunkten ist die Ersparnis enorm. Aus 10¹² Rechenschritten für eine Million Datenpunkte bleiben nur noch 20·10₆ übrig. Ein 3,5 Gigahertz-Rechner bräuchte dafür nur noch wenige Millisekunden. Der Mathematiker taufte seinen Algorithmus ganz kreativ »Fast-Fourier-Transform«. Inzwischen wird er zu den wichtigsten Programmcodes der Welt gezählt.

Als der Physiker Richard Garwin erkannte, was Tukey da auf seinen Zetteln rechnete, wollte er wissen, wann dieser das veröffentlichen würde. Garwin war das Potenzial der Methode sofort bewusst. Tukey antwortete, er arbeite mit einem Informatiker an der Implementierung, es würde aber wohl noch ein paar Jahre dauern. Damals hatten die Rechner nur wenig Speicher, was es knifflig machte, den Algorithmus in solchen Maschinen umzusetzen. Garwin kam das trotzdem viel zu lang vor, weshalb er vorschlug, selbst nach einem Informatiker zu suchen, der das Problem schneller lösen könnte.

Er setzte sich daher mit dem Computerwissenschaftler Jim Cooley in Verbindung. »Garwin erzählte mir, er hätte ein wichtiges Problem, das mit Periodizitäten in einem 3-D-Kristall von Helium-3 zusammenhängt. Erst später erfuhr ich, dass er die seismische Fernüberwachung verbessern wollte, um ein Verbot von Kernwaffentests zu erleichtern«, schrieb Cooley 1987. »Zu dieser Zeit hatte ich die Experimente zu Helium-3 schon längst gemacht und war um die Fourier-Transformation herumgekommen«, gab Garwin zu. Zunächst schenkte Cooley dem neuen Forschungsprojekt nicht allzu viel Aufmerksamkeit und konzentrierte sich auf seine eigenen Arbeiten. Doch die Hartnäckigkeit von Garwin, der ihn und seinen Vorgesetzten immer wieder anrief, um nach den Fortschritten zu fragen, führte dazu, dass Cooley dem Vorhaben hohe Priorität einräumte. Dennoch dauerte es einige Monate, bis Cooley zusammen mit Tukey 1965 den Algorithmus veröffentlichte – zwei Jahre nachdem sich die Sowjetunion und die USA geeinigt hatten, auf alle Atomtests bis auf jene im Untergrund zu verzichten.

Teile und herrsche!

Die Fast-Fourier-Transformation basiert auf dem altgedienten Prinzip: Teile und herrsche. Die Sinus- und Cosinusfunktionen haben viele Symmetrien, die man ausnutzen kann, wenn man die Datenpunkte geschickt unterteilt. Angenommen, acht Datenpunkte liegen in gleichmäßigem Abstand auf der x-Achse mit den Koordinaten 0, 1, 2, …, 7. Für diese zeichnet man nun alle möglichen Cosinusfunktionen ein (für die Sinusfunktionen ergibt sich ein ähnlicher Zusammenhang): cos(0·2πx/8) = 1, cos(2πx/8), cos(4πx/8), …, cos(14πx/8). Dabei lassen sich gewisse Muster erkennen. Beim mittleren Datenpunkt x = 4 haben beispielsweise alle Funktionen mit gerader Frequenz den gleichen Wert: cos(0·2π·4/8) = 1, cos(2π) = 1, cos(4π) = 1, cos(6π) = 1. Auch die ungeraden Frequenzen liefern ein gleiches Ergebnis: cos(π) = −1, cos(3π) = −1, cos(5π) = −1, cos(7π) = −1. Anstatt den mittleren Datenpunkt also mit acht Funktionen zu multiplizieren, muss man nur zwei Produkte bilden. Ähnliche Zusammenhänge ergeben sich bei den anderen Datenpunkten. Auf diese Weise kann man die ursprünglich angedachten 8·8 = 64 Rechenschritte auf 8·log₂8 = 24 eindampfen.

Damit lässt sich ein systematisches Verfahren für N Datenpunkte entwickeln (hier beispielhaft für Sinusfunktionen skizziert): Zunächst nummeriert man die Datenpunkte von 0 bis N−1 durch. Dann betrachtet man immer zwei Sinusfunktionen sin(2πfx/N) für die Frequenzpaare: f = 0 und f = N/2, f = 1 und f = (N/2+1), …, f = (N/2−1) und f = N−1. Im ersten Schritt vergleicht man die beiden Sinusfunktionen für f = 0 und f = N/2: sin(2π·0·x/N) und sin(2π·N·x/(2N)). Beide Sinusfunktionen liefern für gerade Datenpunkte (x = 2n) immer den Wert 1. Für f = 1 und N/2+1 ergibt sich sin(2π·x/N) und sin(2π·N·x/(2N) + 2π·x/N) = sin(π·x + 2π·x/N). Für gerade x = 2n entspricht der letzte Term bloß einer Sinusfunktion, die um ein ganzzahliges Vielfaches n von 2π verschoben ist. Eine um 2π verschobene Sinusfunktion entspricht der ursprünglichen Sinusfunktion. Daher liefern auch diese beiden Funktionen für gerade Datenpunkte stets denselben Wert. Man kann sich davon überzeugen, dass für die übrigen Frequenzen dasselbe gilt. Für die ungeraden Punkte ergibt sich ein ähnlicher Zusammenhang: Die paarweisen Werte der Sinus- und Cosinusfunktionen sind allerdings nicht identisch, sondern an der x-Achse gespiegelt – das heißt, sie unterscheiden sich um ein Vorzeichen.

Das kann man ausnutzen: Anstatt jeden Datenpunkt mit jeder Sinus- und Cosinusfunktion zu multiplizieren, kann man den Aufwand halbieren. Dafür teilt man die Datenpunkte in zwei Gruppen auf und muss jeden Punkt mit nur jeweils halb so vielen Funktionen multiplizieren. Teile und herrsche. Doch wir sind an mehr als einer bloßen Halbierung der Rechenschritte interessiert: Wenn man statt 10¹² noch 5·10¹¹ Berechnungen durchführen muss, hat man nicht allzu viel gewonnen. Der Schlüssel liegt in der wiederholten Ausführung des Tricks.

Den Aufwand immer wieder halbieren

Das heißt: Im zweiten Schritt werden die geraden und die ungeraden Datenpunkte halbiert. Dadurch ergeben sich vier Gruppen, in denen man nach Mustern für die trigonometrischen Funktionen suchen kann. Das wird etwas kniffliger, man muss dazu das Reich der reellen Zahlen verlassen und ebenfalls Wurzeln aus negativen Zahlen zulassen. Doch das Ergebnis ist das gleiche: Die Anzahl der Berechnungen halbiert sich. Und man kann weitermachen, indem man auch diese vier Gruppen unterteilt und daraus acht mit jeweils halb so vielen Punkten macht. Den Prozess wiederholt man so lange, bis nur noch ein einziger Datenpunkt in jeder Gruppe vorhanden ist – bei N Datenpunkten kann man die Punkte maximal log₂-mal halbieren. In jedem dieser Schritte muss man dann noch N Berechnungen durchführen, dadurch ergeben sich insgesamt Nlog₂N Rechenschritte.

Auch wenn sich Tukey die Idee hinter der Fast-Fourier-Transformation eigenständig erarbeitet hat, war er nicht der Erste. Es gibt Aufzeichnungen von Carl Friedrich Gauß (1777–1855), die belegen, dass er ebenfalls bereits 1805 eine solche Methode ausgearbeitet hatte – noch bevor Joseph Fourier (1768–1830) seine Theorie vorstellte. Allerdings erachtete Gauß sein Ergebnis wohl nicht als bedeutend genug, um es zu veröffentlichen. Da er zudem eine veraltete Notation genutzt und alles auf Latein notiert hatte, geriet die Methode in Vergessenheit und wurde erst im 20. Jahrhundert wiederentdeckt.

Mit der Fast-Fourier-Transformation haben Cooley und Tukey einen Algorithmus geschaffen, der die Wissenschaft revolutioniert hat. So lässt sich heute beispielsweise beurteilen, ob Nordkorea Atomwaffen testet. Aber auch alle anderen Aufgaben, die mit der Signalverarbeitung zu tun haben, lassen sich mit dem Algorithmus meistern: zum Beispiel die Kompression von Daten. Wenn Sie also das nächste Mal ein Hundebild googeln, Ihren Lieblingssong auf Spotify hören oder eine Serie streamen, können Sie der raffinierten Fast-Fourier-Transformation dankbar sein.

​​Was ist euer Lieblingsmathetheorem? Schreibt es gerne in die Kommentare – und vielleicht ist es schon bald das Thema dieser Kolumne!