Die fabelhafte Welt der Mathematik: Homer Simpson widerlegt einen der größten Mathematiker der Geschichte

Der Plot von »Im Schatten des Genies« klingt nach einer typischen »Simpsons«-Folge: Der Antiheld der beliebten US-amerikanischen Zeichentrickserie, Homer Simpson, kämpft darin mit einer Midlife-Crisis. Wie er enttäuscht feststellt, hat er in seinem Leben noch nichts Nennenswertes geleistet. Daher beschließt Homer, dem berühmten Erfinder Thomas Edison nachzueifern, und versucht seinerseits technische Neuheiten zu entwickeln, was natürlich in einem Desaster endet. Doch wer die 1998 erstmals ausgestrahlte Folge aufmerksam verfolgt, erlebt eine Überraschung – zumindest, wenn man sich mit Mathematik auskennt.
Denn bei genauerem Hinsehen sticht in einer Szene ein besonderes Detail heraus: Homer steht – ganz im Stil eines nerdigen Professors – nachdenklich mit Brille an einer vollgekritzelten Tafel. Neben den obligatorischen Donuts, die nicht nur Homers Leibspeise sind, sondern gerade im Bereich der Topologie eine große Rolle spielen, findet sich eine harmlos anmutende Gleichung: 398712 + 436512 = 447212. Tippt man sie in einen Taschenrechner ein, erweist sie sich offenbar als richtig. Das Erstaunliche: Sie widerspricht einem der etabliertesten Theoreme der Mathematik, dem großen Satz von Fermat.
Der große Satz von Fermat: Ein jahrhundertealtes mathematisches Rätsel
Dieser stammt aus dem 17. Jahrhundert und sieht auf den ersten Blick recht einfach aus: Er besagt, dass die Gleichung xn + yn = zn keine ganzzahligen, positiven Lösungen x, y und z hat, wenn n größer ist als zwei. Wählt man n = 1, dann ist die Gleichung immer erfüllt: Egal, wie man die Werte für x und y wählt, z wird stets ein positives, ganzzahliges Ergebnis sein, zum Beispiel: 3 + 6 = 9. Selbst Homer, der in der Serie häufig als dümmlich dargestellt wird, traut man diese Einsicht zu.
Für n = 2 wird es schon etwas kniffliger, denn die Gleichung wird quadratisch: x2 + y2 = z2. Wenn x und y ganzzahlige Werte haben, muss das nicht notwendigerweise für z gelten, etwa ergibt für x = 1 und y = 2 die Formel 12 + 22 = 5 - und 5 ist keine Quadratzahl. Das heißt, es gibt zwar eine Lösung für z (die Wurzel aus 5), die ist jedoch nicht ganzzahlig. Dennoch findet man Ausnahmen, für welche die quadratische Gleichung doch eine passende Lösung hat, zum Beispiel: 42 + 32 = 25 = 52. 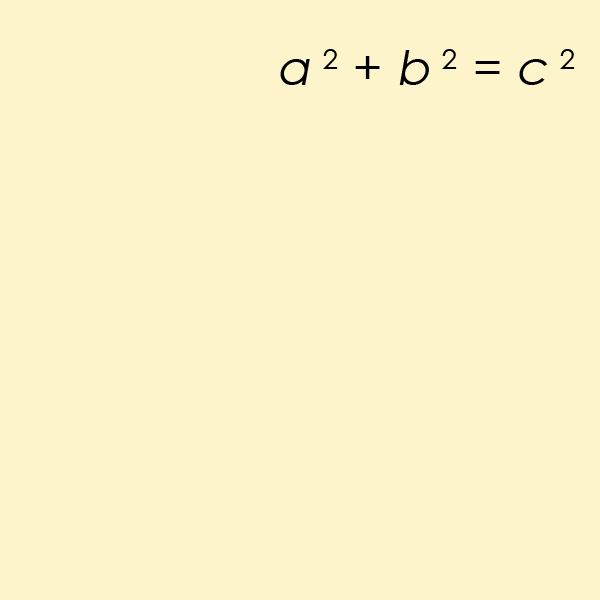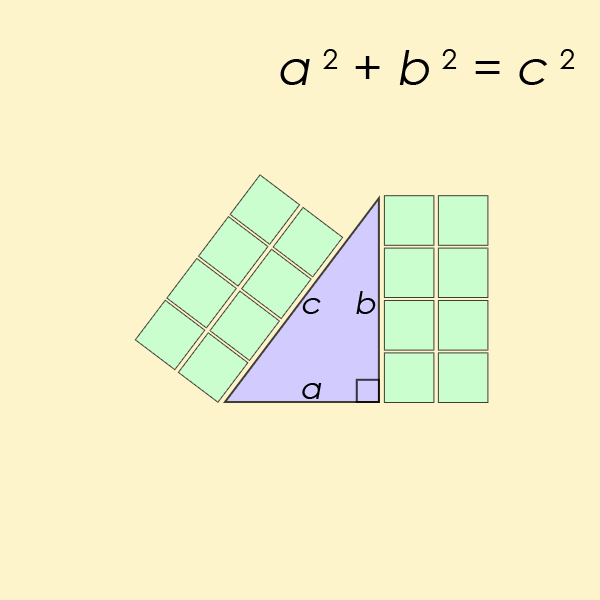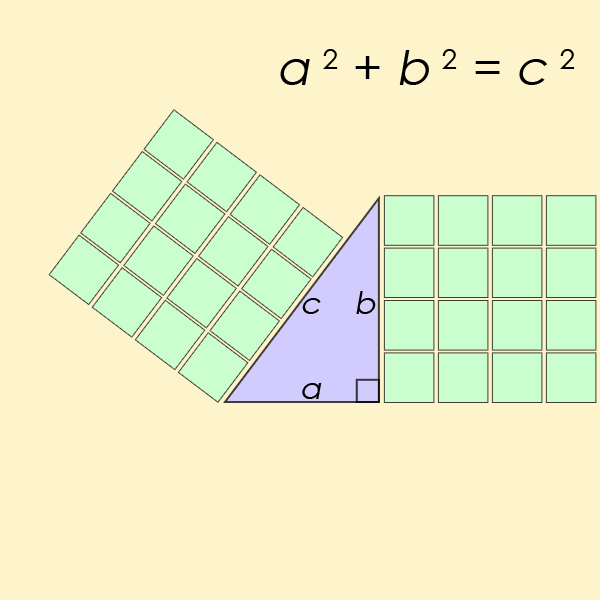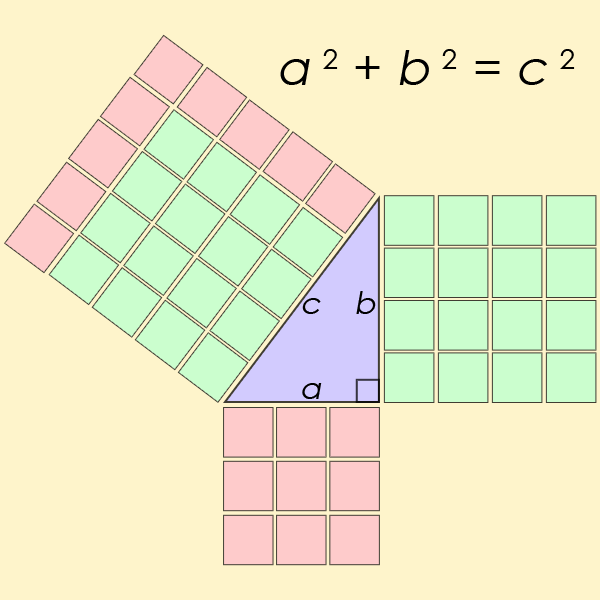
Das lässt sich geometrisch interpretieren, ganz im Sinne von Pythagoras, dessen berühmte Formel Schülerinnen und Schüler wie Lisa und Bart Simpson in der Mittelstufe begegnet: Wenn x2 + y2 = z2 ganzzahlige Lösungen x, y und z besitzen, dann gibt es rechtwinklige Dreiecke, deren Seitenlängen x, y und z ebenfalls ganzzahlige Werte haben. Und wie sich herausstellt, gibt es davon unendlich viele.
Sobald man die Gleichung aber für n = 3 betrachtet, findet man für x3 + y3 = z3 erstaunlicherweise keine einzige ganzzahlige Lösung mehr. Das bedeutet, man kann einen Würfel mit ganzzahligen Seitenlängen z nicht in zwei weitere Würfel aufteilen, die ebenfalls ganzzahlige Seitenlängen (x und y) besitzen. Gleiches gilt für alle weiteren Werte von n.
Fermat behauptet in einer Randnotiz, einen Beweis gefunden zu haben
Der französische Gelehrte Pierre de Fermat (1607–1665) erkannte das schon früh – und behauptete in einer Randnotiz, das auch belegen zu können. In einem Buch des antiken Wissenschaftlers Diophantos von Alexandria notierte er in Latein: »Ich habe hierfür einen wahrhaft wunderbaren Beweis entdeckt, doch ist dieser Rand hier zu schmal, um ihn zu fassen.« Es war nicht das erste Mal, dass Fermat das tat. Tatsächlich hinterließ er zahlreiche ähnliche Hinweise an anderen Stellen. Alle davon konnten andere Fachleute beweisen.
Davon überzeugt, dass auch dieser Beweis einfach zu finden sei, versuchten sich etliche Mathematikerinnen und Mathematiker, darunter namhafte Größen wie Leonhard Euler oder Ernst Eduard Kummer, daran – und scheiterten. Denn wie in dem abstrakten Fach üblich, lässt sich ein Problem nicht notwendigerweise leicht lösen, nur weil es einfach zu formulieren ist.
Tatsächlich dauerte es mehr als 350 Jahre, bis das Rätsel geknackt wurde. Der Geniestreich gelang Andrew Wiles 1994, der das Geheimnis um Fermats großen Satz lüftete. Seine eindrucksvolle Arbeit schlug hohe Wellen: Er entwickelte neuartige Methoden, die zu weiteren bahnbrechenden Entdeckungen in dem Bereich führten. Dafür wurde er unter anderem 2016 mit dem Abelpreis geehrt, einer der höchsten Auszeichnungen in der Mathematik.
Für den Beweis muss man die Algebra, die man aus der Schule kennt, verlassen und in verzweigtere mathematische Gebiete eindringen. Gerhard Frey stellte 1984 die Vermutung auf, dass man aus den Lösungen x, y und z der Gleichung xn + yn = zn für n > 2 eine seltsame Art von Kurve konstruieren könnte: eine elliptische Kurve, für die es allerdings keine Darstellung als Modulform gebe – eine höchst symmetrische Funktion, die im Reich der komplexen Zahlen (mit Wurzeln aus negativen Zahlen) existiert.
Eine andere Vermutung besagt jedoch, dass jede elliptische Kurve sich als Modulform darstellen lässt. Nachdem Ken Ribet 1986 Freys Hypothese bewies, blieb noch die zweite offen: Man musste zeigen, dass jede elliptische Kurve eine dazugehörige Modulform besitzt. Wiles gelang es Mitte der 1990er Jahre, auch diese Lücke zu schließen und damit Fermats großen Satz zu beweisen.
Eine Frage bleibt dabei aber offen: Fermat konnte vor mehr als drei Jahrhunderten nichts von den mathematischen Zusammenhängen gewusst haben, die Wiles in seiner Veröffentlichung genutzt hat. Elliptische Kurven und Modulformen waren damals noch nicht bekannt. Hatte sich der Gelehrte mit der Randnotiz einen Scherz erlaubt? Oder hatte er nur geglaubt, einen Beweis gefunden zu haben, und sich verrechnet? Es gibt noch eine dritte Möglichkeit: Eventuell existiert eine wesentlich einfachere Beweismethode, die bisher noch niemand gefunden hat.
Widerlegt Homer Simpson den großen fermatschen Satz?
Dass Wiles' Ansatz richtig ist, zweifelt niemand ernsthaft an. Seinen Fachaufsatz haben viele Expertinnen und Experten geprüft, zumal einige seiner Techniken immer wieder aufgegriffen werden, um andere mathematische Zusammenhänge zu offenbaren. Das schmälert die Wahrscheinlichkeit, dass sich irgendwo ein Fehler eingeschlichen haben könnte.
Wie kann es aber sein, dass Homer Simpson in der beliebten TV-Serie ganz beiläufig eine Gleichung an eine Tafel kritzelt, die offenbar den großen Satz von Fermat widerlegt? Schließlich stellt 398712 + 436512 = 447212 eine ganzzahlige Lösung der Gleichung xn + yn = zn für n = 12 dar – und die darf es eigentlich gar nicht geben.
Glücklicherweise lässt sich das Rätsel schnell aufklären. Wenn man die zwölfte Potenz einer vierstelligen Zahl berechnet, entsteht ein enorm großer Wert, der aus 43 Ziffern besteht. Gewöhnliche Taschenrechner können damit nicht umgehen, ihr Display besitzt meist nur zehn Stellen, weshalb sie die Zahlenwerte auf- oder abrunden. Wenn man allerdings einen genaueren Rechner oder ein Computerprogramm nutzt, stellt man fest, dass die Ergebnisse nicht exakt übereinstimmen. Zum Beispiel ist 398712 + 436512 = 4472,000000007057617187512 eine bessere Näherung der tatsächlichen Lösung, die wesentlich komplizierter ist.
Fermat hatte doch Recht
In Wirklichkeit gibt es demnach keine positive ganzzahlige Zahl z, welche die Gleichung 398712 + 436512 = z12 löst. Das eigentliche Problem lag also nicht bei Fermat oder Wiles, sondern beim begrenzten Auflösungsvermögen herkömmlicher Taschenrechner.
Natürlich dürfte Homers Formel echte Mathematiker und Mathematikerinnen nicht wirklich verwundert haben, da Rundungsfehler bei elektronischen Geräten nichts Neues sind. Erstaunt hat die Fachleute wohl eher, dass ein solcher Inhalt überhaupt in den »Simpsons« auftaucht, einer Serie, die eigentlich nichts mit Mathematik am Hut hat. Zufällig ist dieses Tafelbild nicht entstanden, denn es braucht einiges an Hintergrundwissen, um diese Beinahe-Lösung zu finden.
Eine weitere Überraschung dürfte sein, dass viele Autoren der Fernsehserie studierte Informatiker, Mathematiker oder Physiker sind, darunter David X. Cohen, der für den Fermat-Witz verantwortlich ist. Er hatte zu dem Zweck extra ein Computerprogramm geschrieben, das ihm die Beinahe-Lösung ausspuckte. Dass er sich gerade für den großen Satz von Fermat entschied, mag nicht reiner Zufall gewesen sein: Tatsächlich besuchte Cohen als Student Vorlesungen von Ken Ribet, der die Vorarbeit zu Wiles' Beweis geleistet hatte, indem er die Vermutung von Frey bewiesen hatte.
»Im Schatten des Genies« ist daher bei Weitem nicht die einzige Folge, in der die Autoren der »Simpsons« unauffällig Nerd-Witze untergebracht haben. In seinem Buch »Homers letzter Satz« präsentiert der Mathematiker Simon Singh viele weitere unterhaltsame Beispiele. Ob die Produzenten damit wohl das allgemeine Interesse an dem unbeliebten Fach steigern wollten? Jedenfalls lädt es dazu ein, beim gemütlichen Fernsehabend künftig etwas genauer hinzuschauen – womöglich macht man dabei eine mathematische Entdeckung.
Was ist euer Lieblingsmathetheorem? Schreibt es gerne in die Kommentare – und vielleicht ist es schon bald das Thema dieser Kolumne!
Schreiben Sie uns!
6 Beiträge anzeigen