Wie vermutlich jedes Kind habe ich früher gerne am Lichtschalter gespielt und Lampen schnell hintereinander ein- und ausgeschaltet. Doch irgendwann griff meine Mutter ein und sagte mir, ich solle das unterlassen, weil die Glühbirne davon schneller kaputt gehe. Stellen Sie sich nun vor, Sie ignorieren die Warnung und toben sich mit einer Lampe aus: Sie schalten sie ein, eine Minute später aus, nach einer halben Minute wieder ein, nach 15 Sekunden aus und so weiter. Sie halbieren nach und nach die Zeitintervalle, so dass der Zustand der Lampe immer schneller wechselt. Wird die Glühbirne (oder LED) nach zwei Minuten leuchten oder nicht?

Diese vermeintlich einfache Frage hat in der Vergangenheit zu heftigen Diskussionen geführt. Grund dafür ist, dass der Lichtschalter nach zwei Minuten unendlich oft ein- und ausgeschaltet wurde. Die Zeitabstände zwischen dem Wechsel werden immer kleiner – bis sie nach zwei Minuten null betragen. Der britische Philosoph James F. Thomson, der sich das Gedankenexperiment 1954 überlegt hat, kam zu folgendem Schluss: »Es scheint unmöglich, die Frage zu beantworten. Die Lampe kann nicht an sein, denn ich habe sie nie eingeschaltet, ohne sie gleich wieder auszuschalten. Sie kann aber auch nicht aus sein, weil ich sie zuerst eingeschaltet habe und sie danach nie wieder ausgeschaltet habe, ohne sie gleich wieder einzuschalten. Aber die Lampe muss entweder an oder aus sein. Das ist ein Widerspruch.«

Doch nicht nur Philosophen haben sich den Kopf über das Problem zerbrochen. Denn ursprünglich stammt die Überlegung aus dem Jahr 1703, als sich der italienische Gelehrte Guido Grandi (1671–1742) mit unendlichen Reihen beschäftigte. Diese bezeichnen Summen mit unendlich vielen Additionen, etwa: 1 + ½ + ¼ + ⅛ + und so weiter. Egal, wie viele der Terme man zusammenrechnet, das Ergebnis ist stets kleiner als zwei. Mathematikerinnen und Mathematiker sagen daher, der »Grenzwert« der Reihe beträgt zwei. Das ist der Grund, warum man im geschilderten Gedankenexperiment nur zwei Minuten braucht, um den Schalter einer Lampe unendlich oft zu betätigen.

Die Grandi-Reihe stiftet Verwirrung

Grandi widmete sich in seiner Arbeit allerdings einer Reihe, die weitaus mehr Fragen aufwirft: 1 − 1 + 1 − 1 + 1 − …. Abwechselnd zieht man eine Eins ab und addiert sie gleich darauf wieder. Assoziiert man »1« mit dem Einschalten einer Lampe und »−1« mit dem Ausschalten, kommt man in Kombination mit den verkürzten Zeitabständen auf das oben erwähnte Paradoxon der Thomson-Lampe.

Diesem liegt die Frage zu Grunde, welchen Wert man erhält, wenn man die Terme plus und minus eins unendlich oft summiert. Die ersten zwei Glieder ergeben null, addiert man das dritte, kommt eins heraus, zuzüglich des vierten kommt man wieder auf null, anschließend auf eins und so weiter. Berücksichtigt man eine gerade Anzahl an Summanden, ist das Ergebnis null, bei ungeraden jedoch eins. Aber wie ist das im Unendlichen? Ist unendlich eine gerade oder ungerade Zahl?

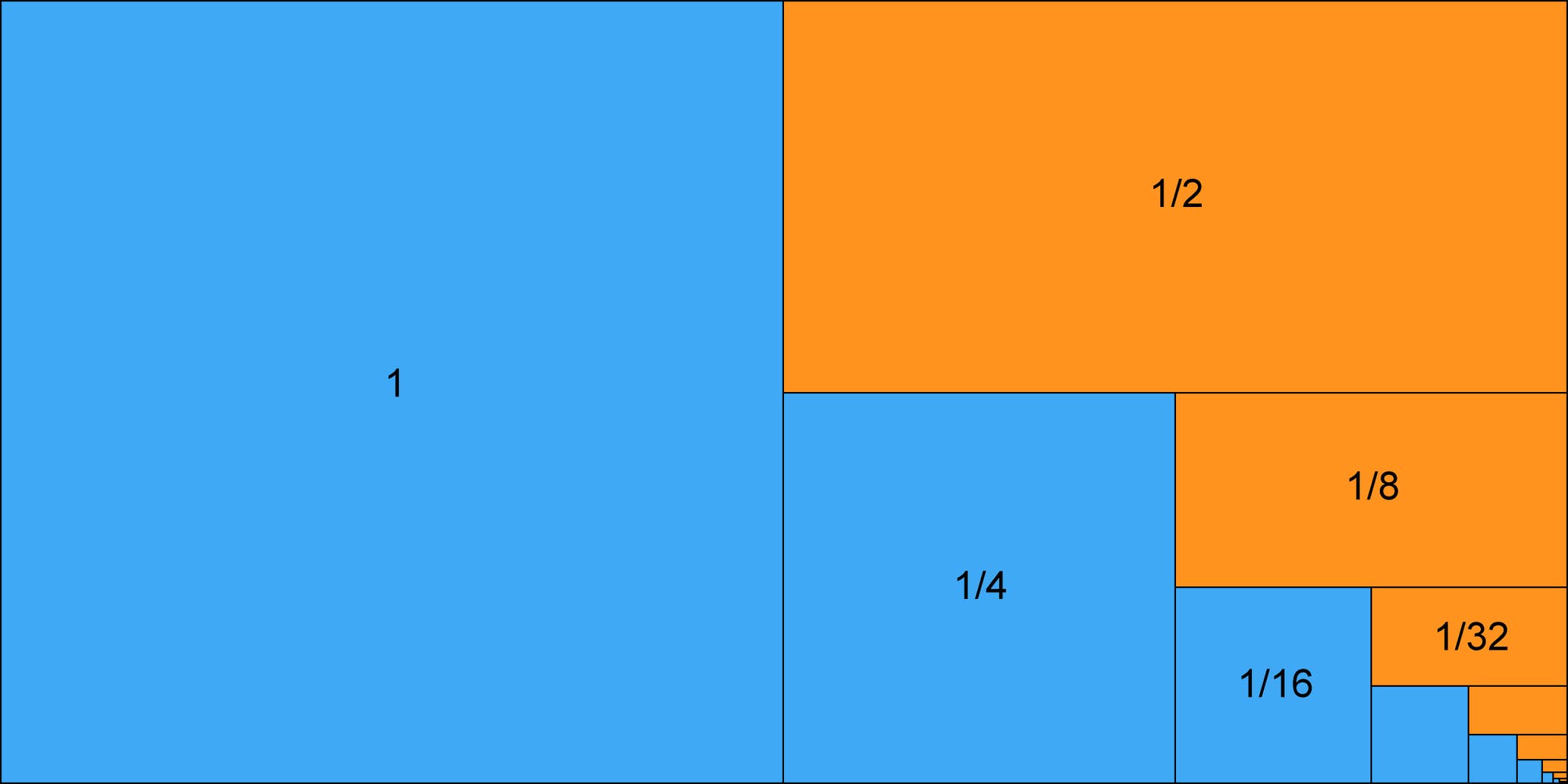
Dass solche Überlegungen nicht weiterführen, erkannte Grandi schnell. Daher untersuchte er die Reihe genauer. Indem man geschickte Klammern setzt, erhält man eine unendliche Summe aus Nullen: (1 − 1) + (1 − 1) + (1 − 1) + und so weiter. Daher müsste der Grenzwert null betragen, die Lampe ist am Ende also aus.

Verschiebt man die Klammern allerdings um eine Stelle nach rechts, erhält man einen anderen Grenzwert: 1 + (−1 + 1) + (−1 + 1) + (−1 + 1) + …= 1, die Lampe wäre am Ende eingeschaltet. Wieder hat man also zwei Ergebnisse zur Auswahl: null oder eins. Um alles noch verwirrender zu machen, fand Grandi ein weiteres mögliches Ergebnis: ½.

Ein Kompromiss als Lösung: Halb ein, halb aus?

Das Resultat ist extrem überraschend, da die Summe nur aus ganzzahligen Zahlen besteht. Wie kann man so auf einen gebrochenzahligen Wert kommen? Dafür schrieb Grandi die unendliche Reihe auf und gab dem Grenzwert den Namen S: S = 1 − 1 + 1 − 1 +…. Dann klammerte er den ersten Summanden aus und stellte fest: S = 1 − (1 − 1 + 1 − 1 +…)= 1 − S. Er kam also auf die simple Gleichung S = 1 − S, woraus S = ½ folgt. Und tatsächlich sind auch heute viele Fachleute davon überzeugt, dass dieses Ergebnis richtig ist – dafür gibt es mehrere Gründe.

Möchte man den Grenzwert einer Reihe bestimmen, gibt es in der Mathematik eine klar vorgeschriebene Vorgehensweise. Man betrachtet die Folge a_n, die sich aus den ersten n Summanden ergibt, und bestimmt deren Grenzwert. Für die Reihe 1 + ½ + ¼ + ⅛ + … wäre die entsprechende Folge: a₁ = 1, a₂ = 1 + ½ = ³⁄₂, a₃ = 1 + ½ + ¼ = ⁷⁄₄ und so weiter. Für das n-te Folgenglied erhält man den Wert: a_n = 2 − (½)ⁿ. Je größer n wird, desto kleiner wird der Term (½)ⁿ, so dass der Grenzwert von a_n zwei ist.

Diese Methode lässt sich nicht auf die Grandi-Reihe anwenden, da die Folge der »Partialsummen« a_n nicht konvergiert: Die Folgenglieder a_i nehmen abwechselnd die Werte null und eins an. Man kann sich jedoch eines gängigen Tricks bedienen und eine neue Folge c_n definieren, die aus den Mittelwerten der Partialsummen a_n besteht: c₁ = a₁, c₂ = ½·(a₁ + a₂), c₃ = ⅓·(a₁ + a₂ + a₃) und so weiter. Wenn man dieses Verfahren für die einfache konvergente Reihe 1 + ½ + ¼ + ⅛ + … berechnet, kommt man auf den gleichen Grenzwert wie zuvor, nämlich zwei. Für die Grandi-Reihe erhält man auf diese Weise ebenfalls einen eindeutigen Grenzwert: c₁ = 1, c₂ = ½·(1 + 0) = ½, c₃ = ⅓·(1 + 0 + 1) = ⅔ und so weiter. Wenn man den Grenzwert dieser Folge auswertet, landet man bei ½.

Dieses Argument überzeugt viele Fachleute davon, dass ½ der tatsächliche Grenzwert der Grandi-Reihe ist. Doch was bedeutet das für das Gedankenexperiment mit der Thomson-Lampe? Ist der Raum nach Ablauf der zwei Minuten halb beleuchtet und halb dunkel? Für jeden noch so kurzen Augenblick, bevor die Zeitspanne abgelaufen ist, kann man den Zustand der Lampe beschreiben. Doch bei genau zwei Minuten bleibt das Ergebnis ein Rätsel. Um dieses besser zu beleuchten, haben die Physikphilosophen John Earman und John D. Norton das Gedankenexperiment in eine etwas realere Umgebung gerückt.

Eine halbwegs realistische Umsetzung des Gedankenexperiments

Angenommen, eine Metallkugel wird auf einem induktionsfähigen Kochfeld fallen gelassen. Zunächst ist die Kugel eine Minute in der Luft, anschließend 30 Sekunden, dann nur noch 15 und so weiter. Sie dotzt zwei Minuten lang unendlich oft auf und erzeugt dabei jedes Mal einen elektrischen Impuls in der Platte. Diese sei dabei mit einer Lampe verbunden, die bei jedem Kontakt aufleuchtet. Da die Kugel nach zwei Minuten durch die Schwerkraft auf der Metallplatte zum Erliegen kommt, ist die Lampe am Ende eingeschaltet. Damit hätte das Lager Recht, das behauptet, der Grenzwert läge bei eins.

Aber man kann die Situation umkehren: Wenn die auftreffende Kugel nicht den Stromkreis zwischen Lampe und Induktionsfeld schließt, sondern öffnet. In diesem Fall leuchtet die Lampe und wird immer dann ausgeschaltet, wenn die Kugel auf der Platte landet. Nach dem Ablauf der zwei Minuten ist die Lampe also aus. Nach dieser Interpretation beträgt der Grenzwert der Grandi-Reihe null. Norton und Earman kommen daher zu dem Schluss: »Die Thomson-Lampe ist kein Paradox, sondern ein Problem, das unvollständig beschrieben ist.«

Folgt man streng der mathematischen Definition für den Grenzwert einer Reihe, dann gibt es nur einen Schluss: Es gibt keinen Grenzwert, das heißt die Grandi-Reihe divergiert. Erweitert man das Konzept hingegen (so, wie man beispielsweise die reellen Zahlen um Wurzeln aus negativen Zahlen erweitert), halten die meisten Fachleute an ½ als Lösung fest – auch wenn sich damit nicht erklären lässt, wie Thomsons Gedankenexperiment ausgeht.

Und um das Chaos vollständig zu machen, gibt es auch einige Personen, die auf einen völlig anderen Grenzwert beharren, der weder 0 noch 1 oder ½ ist. Denn es gibt auch plausible Berechnungen, die nahelegen, dass die Grandi-Reihe gegen den Wert ⅔ konvergiert. Dazu kann man sich etwa die Gleichung (1 + x)/(1 +x + x²) = 1 − x² + x³ − x⁵ + x⁶ − x⁸ + … ansehen. Wenn man x = 1 setzt, entspricht die rechte Seite der Grandi-Reihe und die linke dem Wert ⅓.

Damit bleibt das Rätsel um die Thomson-Lampe ungelöst. Um auf der sicheren Seite zu bleiben, kann man argumentieren, dass sich ein solches Gedankenexperiment niemals umsetzen lässt: Denn weder ein Mensch noch eine Metallkugel können in der realen Welt dafür sorgen, dass eine Lampe innerhalb von zwei Minuten tatsächlich unendlich oft aufleuchtet. Oder man hört ganz einfach auf die Warnungen der Eltern und lässt das Ein- und Ausschalten ganz bleiben.

Was ist euer Lieblingsmathetheorem? Schreibt es gerne in die Kommentare – und vielleicht ist es schon bald das Thema dieser Kolumne!