Lexikon der Mathematik: n-Eck
auch Polygon genannt, geschlossener Streckenzug mit n Eckpunkten A1, A2 ... An.
Ein n-Eck heißt windschief, falls seine Eckpunkte nicht in einer Ebene liegen; ansonsten handelt es sich um ein ebenes n-Eck. Falls es außer den Eckunkten keine weiteren gemeinsamen Punkte zweier Seiten eines ebenen n-Ecks gibt, so handelt es sich um ein einfaches n-Eck, anderenfalls um ein überschlagenes n-Eck, falls sich zwei nicht aufeinanderfolgende Strecken in einem Punkt schneiden, sowie um ein nicht überschlagenes n-Eck, falls ein Eckpunkt auf einer ihm nicht benachbarten Strecke liegt.
Nicht einfaches überschlagenes n-Eck
Nicht einfaches nicht überschlagenes n-Eck
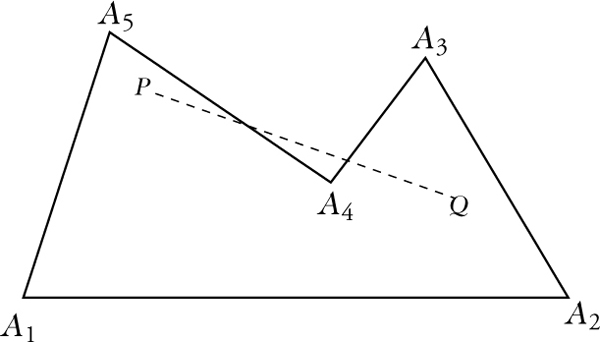
Jedes einfache ebene n-Eck teilt die Ebene in zwei Teile (das Innere und das Äußere des n-Ecks), die durch die Gesamtheit der Seiten des n-Ecks voneinander getrennt sind. Ein einfaches n-Eck heißt konvex, falls Verbindungsstrecken beliebiger Punkte P und Q des Inneren des n-Ecks nur innere Punkte enthalten und ansonsten konkav.
Konvexes n-Eck
Konkaves n-Eck
Die Summe der Längen der Seiten heißt Umfang eines n-Ecks. Verbindungsstrecken zweier nicht benachbarter Eckpunkte eines n-Ecks werden auch als Diagonalen bezeichnet. Von jedem Eckpunkt gehen (n − 3) Diagonalen aus, nämlich zu allen Eckpunkten außer der betrachteten Ecke selbst und den beiden benachbarten Ecken. Jedes n-Eck besitzt somit (da jede Diagonale von zwei Eckpunkten aus gezählt werden kann) insgesamt
\begin{eqnarray}\frac{n(n-3)}{2}\end{eqnarray}
Diagonalen.
Die Summe der Größen der Innenwinkel eines n–Ecks hängt einzig und allein von der Zahl n der Ecken ab, siehe Winkelsumme im n-Eck.
Ein konvexes n-Eck heißt regelmäßig, regulär oder gleichseitig, falls alle seine Seiten gleich lang sind (Gauß, Satz von, über n-Ecke).



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.