Lexikon der Mathematik: Pareto-Verteilung
das für k > 0 und a > 0 durch die Wahrscheinlichkeitsdichte
Die zugehörige Verteilungsfunktion ist durch
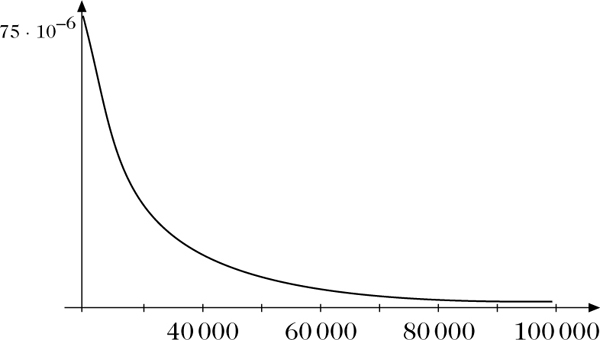
Dichte einer Pareto-Verteilung mit Parametern k = 20000 und a = 1.5
Für eine mit den Parametern k und a Paretoverteilte Zufallsvariable X existieren die Momente der Ordnung r, falls r< a ist. Insbesondere ist für a > 1 der Erwartungswert von X durch
Als Konzentrationsmaße werden häufig der Gini-Koeffizient G und die Lorenz-Kurve L verwendet. Bei einer Pareto-Verteilung mit Parametern k > 0 und a > 1 gilt G = (2a − 1)−1 und L(x) = 1 − (1 − x)(a−1)/a. Die für x ≥ 0 bzw. x > 0 durch die Verteilungsfunktionen Fa,C bzw. Fa,b,C mit
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.