Lexikon der Physik: Renormierung
Renormierung
Gerard 't Hooft, Utrecht, Niederlande
1 Einleitung
Das Konzept der Renormierung ist ein notwendiger Bestandteil in der Festkörpertheorie und der Quantenfeldtheorie zur Beschreibung subatomarer relativistischer Teilchen. Diese Theorien basieren auf einem Satz von Grundgleichungen, die beschreiben, wie die beteiligten Teilchen und/oder Felder in kleinen Abständen miteinander wechselwirken. Die Gleichungen sind für Festkörpersysteme gegeben durch den Hamilton-Operator ![]()
und in der Quantenfeldtheorie durch die Wirkung ![]()
, wobei ![]()
die Lagrange-Dichte ist. Diese Ausdrücke enthalten eine Anzahl von willkürlichen Parametern wie die Masse der Teilchen und die Stärke der wechselwirkenden Kräfte, z.B. derjenigen, die durch die elektrische Ladung ![]()
hervorgerufen werden.
Die Berechnung der Wechselwirkung dieser Teilchen für große Abstände und Zeiten ergibt, daß die Teilchen sich verhalten, als ob ihre Massen und Wechselwirkungskräfte verschieden sind. Diese Unterschiede werden aber durch die Wechselwirkung selbst hervorgerufen. Sind ![]()
bzw. ![]()
die ursprüngliche ›nackte‹ Masse bzw. Ladung bei einem Abstand ![]()
und ![]()
bzw. ![]()
(der Index ›R‹ steht für renormiert) die effektive Masse bzw. Ladung bei einem größeren Abstand ![]()
, so gelten die Beziehungen:
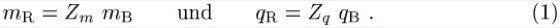
Für die meisten Theorien divergieren die Renormierungskonstanten ![]()
und ![]()
, wenn das Verhältnis der Abstandsskalierung ![]()
gegen Unendlich geht. Aus diesem Grund gibt es keine strenge lokale Definition von ![]()
und ![]()
, wenn ![]()
infinitesimal ist. Dadurch sind die Renormierungskonstanten unendlich groß bzw. schlecht definiert.
Dagegen ist im Fall der klassischen Mechanik die Situation relativ einfach. Newton und Leibnitz fanden heraus, daß unter der Annahme kleiner Zeitschritte ![]()
und entsprechend kleiner Auslenkungen ![]()
das Verhältnis ![]()
wohl definierte Grenzwerte besitzt. Unter dieser Voraussetzung wurde die Theorie der Differentialgleichungen entwickelt. In Festkörpersystemen und in der Quantenfeldtheorie ist die Situation jedoch komplizierter.
2 Kurzer Überblick über die Geschichte der Renormierung
Die heutzutage als Quantenelektrodynamik (QED) bezeichnete Theorie wurde begründet, als M. Born, W. Heisenberg und P. Jordan die Regeln für die Erzeugung und Vernichtung von Teilchen formulierten und P.A.M. Dirac seine berühmten Gleichungen für ein relativistisches Elektron in einem elektromagnetischen Feld aufstellte. Unvermeidlicherweise setzt diese Theorie voraus, daß eine unbegrenzte Anzahl von Teilchen während des Wechselwirkungsprozesses erzeugt und vernichtet werden kann. Je höher die Genauigkeit der Rechnung ist, desto größer wird die Zahl der involvierten Teilchen. Besonders in diesen störungstheoretischen Rechnungen hoher Ordnung tauchen die Schwierigkeiten der ›Unendlichkeiten‹ auf.
Die Tatsache, daß das Strahlungsfeld zur Masse des Elektrons beiträgt, folgt bereits aus den Maxwell-Gleichungen für den Elektromagnetismus, in Kombination mit der Speziellen Relativitätstheorie von Einstein. In diesem Rahmen ergibt sich, daß für eine kleine Murmel mit dem Radius ![]()
seine Masse ![]()
auf

anwachsen würde (in MKS-Einheiten).
Unter der Annahme eines punktförmigen Elektrons ( ![]()
) mit einer physikalischen Masse ![]()
als aktueller Elektronenmasse würde daraus folgen, daß ![]()
negativ und unendlich sein muß – eine sinnlose instabile Situation. In der Quantentheorie kann der Ausdruck ![]()
in erster Näherung durch die Compton-Wellenlänge ![]()
ersetzt werden. Dies entspricht jedoch nicht dem Ergebnis aus der QED, da hier die Divergenz im Gegensatz zu Gl. (2) kein lineares, sondern ein logarithmisches Verhalten in ![]()
zeigt.
Dirac und ebenso W.H. Furry und J.R. Oppenheimer erkannten, daß das starke elektrische Feld in der Nähe des Elektrons zu einer kleinen Trennung der virtuellen Elektron-Positron-Paare führt, und dieser als Vakuumpolarisation bezeichnete Effekt schirmt die Elektronenladung ab. Aufgrund der Vakuumpolarisation ist die wirkliche Elektronenladung ![]()
kleiner als die der ›nackten‹ Ladung ![]()
, und diese Renormierung geht wiederum gegen unendlich und zwar logarithmisch mit ![]()
. In früheren Rechnungen gab es Anhaltspunkte dafür, daß auch die Photonenmasse einer unendlichen Renormierung unterliegt. Da dieses Resultat jedoch der Eichinvarianz widerspricht, wurde es nicht weiter ernst genommen.
Einer der ersten, der verstand, daß alle diese Renormierungen gemeinsam in einem einzigen Programm behandelt werden müssen, war H.A. Kramers. Zusammen mit R.L. de Kronig entwickelte er ein Gleichungssystem, die sogenannten Dispersionsrelationen, die lediglich unter der Annahme, daß Ursache und Wirkung zeitlich geordnet werden müssen, die Berechnung von Effekten höherer Ordnung unter Vermeidung von einigen unendlichen Größen erlaubt. In einer berühmten Konferenz in Shelter Island nahe New York berichtete W. Lamb 1947 über eine anormale Verschiebung von ca. 1000 MHz, die er zwischen dem ![]()
-Zustand und dem ![]()
-Zustand des Wasserstoffatomes gemessen hatte. H. Bethe lieferte nur fünf Tage nach dieser Konferenz eine Erklärung für diesen sogenannten Lamb-Shift, wobei er eine einfache Massenrenormierungstechnik benutzte, dabei allerdings die logarithmische Divergenz bei der Compton-Wellenlänge des Elektrones abschnitt (cut-off). Sein Ergebnis für die Verschiebung war mit 1040 MHz bemerkenswert nahe am gemessenen Wert von Lamb. Die genaue Korrektur zur Ordnung ![]()
wurde zuerst von S. Tomonaga und Co-Autoren berechnet.
Ebenfalls 1947 konnte J. Schwinger erfolgreich die höheren Korrekturterme des magnetischen Moments des Elektrons berechnen, welches durch das gyromagnetische Verhältnis ![]()
(laut Diracs alter Gleichung ist ![]()
) beschrieben wird:
Hierbei ist ![]()
. Das Resultat stimmt gut mit dem experimentellen Wert von 1,00118 überein.
Ein vollständiges Verfahren zur Berechnung aller Korrekturterme zu jeder Potenz von ![]()
wurde von R.P. Feynman, F. Dyson, A. Salam und anderen ausgearbeitet. Ihre Methoden waren streng begrenzt auf die elektromagnetische Wechselwirkung zwischen Elektronen und Photonen. Erst nach und nach wurde die Aufmerksamkeit auch auf andere Wechselwirkungskräfte gelenkt. So etablierte E. Fermi eine Gleichung für die schwache Wechselwirkung, die später von E.C.G. Sudarshan und R.E. Marshak und unabhängig davon von Feynman und M. Gell-Mann verfeinert wurde. Diese Theorie ließ sich jedoch nicht renormieren, was bedeutete, daß sich die unendlichen Terme in ihrer Struktur von den ursprünglichen unterschieden und durch eine Neudefinition der letzteren nicht aufgefangen werden konnten. Die starke Wechselwirkung stellt ein weiteres großes Problem dar: die Kopplungsstärke der starken Kraft ist so groß, daß eine systematische Entwicklung nach den Potenzen dieser Wechselwirkung sinnlos ist.
Die nichtabelsche Eichtheorie, die in der Literatur zuerst von C.N. Yang und R.L. Mills im Jahr 1954 beschrieben wurde, besaß eine Form, die Renormierbarkeit vermuten ließ. Diese Theorie stellt eine direkte Erweiterung der Maxwell-Gleichungen mit einem größeren Satz von Vektorfeldern dar. Der 1964 vorgestellte Englert-Brout-Higgs-Mechanismus deutet auf eine zusätzliche Existenz von Skalarfeldern hin. Mit diesem Ansatz konstruierten S. Weinberg und A. Salam unabhängig voneinander ein Modell für die schwache Wechselwirkung, das renormierbar schien, aber beide waren nicht in der Lage, Rechnungen höherer Störungsordnungen durchzuführen. Zu dieser Zeit wurde die Quantenfeldtheorie jedoch vor allem aufgrund ihrer komplexen Natur, der erforderlichen unendlichen Renormierungen und der entwickelten unrealistischen Theorien abgelehnt. Darüber hinaus ließ sich mit der als Renormierungsgruppe bekannten Technik nicht-störungstheoretisch argumentieren, daß die ›nackten‹ Ladungen oberhalb hoher Energien, also bei kleinen Abständen, unphysikalische Werte besitzen können. L. Landau folgerte, daß physikalisch nicht akzeptable Singularitäten auftreten können.
Der Autor dieses Essays entdeckte 1971, daß Theorien vom Englert-Brout-Higgs-Typ renormierbar sind, und gab eine vollständige Beschreibung zur Berechnung der höheren Ordnungen der Störungsreihe. Zusätzlich fand er heraus, daß die Landau-Singularität nicht in einer Yang-Mills-Theorie der starken Wechselwirkung auftaucht. Diese Besonderheit wurde 1973 von D. Politzer, D. Gross und F. Wilczek wiederaufgenommen und als ›asymptotische Freiheit‹ bezeichnet.
Dieses Renormierungsverfahren ist eindeutig und hinterläßt keine divergenten Terme in den physikalisch meßbaren Größen. Lediglich die ›nackten‹ Parameter, die nicht direkt gemessen werden können, sind divergent. Daraus folgt, daß alle meßbaren Größen der Theorie berechnet werden können, ausgedrückt durch einige frei wählbare Parameter, den physikalischen Konstanten. Eine Schwierigkeit trat in Theorien mit chiralen Wechselwirkungen auf, die unter der Bezeichnung Anomalien bekannt wurde. Dieses Problem wurde unabhängig voneinander von S. Adler und J. Bell sowie R. Jackiw entdeckt. Eine Theorie, die Anomalien besitzt, kann nur renormiert werden, wenn diese Anomalien beseitigt sind. Die Bedingungen zur Beseitigung bilden einfache algebraische Einschränkungen an die Struktur einer Theorie. Später fand man heraus, daß diese Anomalien in Beziehung zu einer nicht-perturbativen Symmetriebrechung stehen, die durch Instantonen hervorgerufen wird. Die Tatsache, daß es keine weiteren Hindernisse gibt, die die Renormierung gefährden, fand seine Bestätigung, als 't Hooft und M. Veltman 1972 ihr Konzept der dimensionalen Renormierung einführten.
Das Standardmodell der Elementarteilchen ist ein spezielles, Anomalie-freies Beispiel für ein Eglert-Brout-Higgs-System und – soweit heutzutage bekannt – in der Lage, alle bekannten Wechselwirkungen zwischen den Elementarteilchen genau zu beschreiben. Bei Energien, die mit den heutzutage eingesetzten Teilchenbeschleunigern noch unerreichbar sind, erwartet man allerdings, daß das Standardmodell beträchtliche Anpassungen erfordert. Abgesehen von den sehr schwachen Effekten aufgrund einer endlichen Neutrinomasse erfordert das gegenwärtige Modell nicht mehr als 20 frei wählbare Konstanten. Zahlreiche Arbeiten der letzten Jahrzehnte bestätigten und verfeinerten das Standardmodell.
3 Feynman-Regeln
Das Gebiet der Quantenfeldtheorie ist zu kompliziert, um in diesem Artikel ausführlich behandelt zu werden. Aus diesem Grund werden wir lediglich eine kurze Zusammenfassung der allgemeinen Ideen geben. Die Teilchen-Wechselwirkung kann verdeutlicht werden, indem jeder Beitrag zur Störungsentwicklung in Form eines Feynman-Diagramms beschrieben wird. Der Propagator für ein skalares Teilchen der Masse ![]()
ist beispielsweise gegeben durch den Ausdruck

Der Term ![]()
würde jedoch die Mehrzahl der Diagramme für große ![]()
-Werte so divergent machen, daß die Theorie nicht renormierbar ist. Nur wenn die Theorie eichinvariant und das betrachtete Vektorteilchen eine Eichboson ist, dessen Masse ![]()
durch Higgs-Mechanismus erzeugt wird, können die Feynman-Regeln derart transformiert werden, daß der Propagator folgende Form erhält:

Hier ist ![]()
ein freier Parameter (der Eichparameter), der meist zu 0 oder 1 gewählt wird. In diesem Fall existieren zusätzliche Geisterfelder, Fadejew-Popow-Geister genannt, die fiktive Beiträge zu den Feynman-Regeln liefern. Sie sehen wie (komplexe) skalare Teilchen aus, stellen aber in Wirklichkeit keine physikalisch beobachtbaren Zustände dar.
Die Gleichheit der Propagatoren (6) und (7) in Kombination mit den notwendigen Beiträgen durch die Fadejew-Popow-Geister folgt aus den Slawnow-Taylor-Identitäten, die die Ward-Identitäten aus der Quantenelektrodynamik verallgemeinern. Im einfachsten Fall stellen die Slawnow-Taylor-Identitäten sicher, daß für die höheren Schleifenkorrekturen (loop corrections) des Propagators eines masselosen Bosons ![]()
gilt. Im Grunde beschreiben die Slawnow-Taylor-Identitäten die Tatsache, daß die Eichfixierung einer Feldtheorie, z.B. durch die Lorentz-Eichung ![]()
, eine neue Symmetrie hervorruft, die von C. Becchi, A. Rouet, R. Stora (und unabhängig davon I.V. Tyutin) entdeckte BRS-Symmetrie.
Die Feynman-Regeln können in einer knappen Form definiert werden, nämlich durch den Lagrange-Dichte ![]()
einer eichfixierten Theorie. Die Propagatoren erhält man aus den Anteilen in der Lagrange-Dichte, die bilinear in den Feldern sind, als das negative Inverse ihrer Fourier-Koeffizienten. Zum Beispiel erhält man den Propagator (4) eines (komplexen) skalaren Teilchens aus dem Term ![]()
. Die Vertizes folgen aus den Termen höherer Ordnung. So entspricht z.B. der Ausdruck ![]()
einem Vertex, der Teilchen 1 mit Teilchen 2 und Teilchen 3 verbindet, mit zu ![]()
proportionaler Amplitude. Anhand genauer Regeln ist es möglich, den Geisterbeitrag zur Lagrange-Dichte aus den eichfixierenden Termen durch die Anwendung infinitesimaler Eichtransformationen auf diese Terme abzuleiten.
4 Renormierbarkeit
Ob eine Theorie störungstheoretisch renormierbar ist, zeigt im Prinzip direkt die Lagrange-Dichte. Die Schwierigkeit besteht gewöhnlich darin, daß zum einen eine eichfixierende Prozedur zu finden ist, die die Lagrange-Dichte in die gewünschte Form überführt, und daß zum anderen die notwendigen Slawnow-Taylor-Identitäten erfüllt sein müssen, damit die verschiedenen Eichfixierungen äquivalent sind. Der letzte Punkt ist besonders wichtig, da die Äquivalenz der verschiedenen Eichungen notwendig ist, um nach der erfolgten Renormierung zu prüfen, ob die erhaltene Theorie unitär und deshalb nützlich zur Beschreibung der realen Welt ist.
Die entscheidende Regel ist ganz einfach, daß alle Propagatoren die Form (4), (5) oder (7), aber nicht (6), besitzen und die Dimension aller Kopplungsparameter in jeder Ordnung gleich oder größer Null ist. Die Dimension bestimmt sich dadurch, daß man der Lagrange-Funktion die Dimension ![]()
(die Anzahl der Dimensionen in Raum und Zeit und im allgemeinen gleich 4), einer Ableitung (oder einem Impuls ![]()
) oder einer Masse ![]()
die Dimension Eins und den Feldern die Dimensionen zuordnet, die zu den bilinearen Termen in ![]()
passen. In der vierdimensionalen Raumzeit besitzen Skalarfelder ![]()
und Vektorfelder ![]()
also die Dimension Eins und Spinorfelder ![]()
die Dimension 3 / 2. Eine Kopplungskonstante, die mit vier Skalar- oder Vektorfeldern multipliziert wird, hat die Dimension Null und eine Konstante, die drei solcher Felder multipliziert (und keine Ableitungen) die Dimension Eins. Wenn nun die obige Bedingung erfüllt ist, erkennt man, daß in den Amplituden höherer Ordnungen nur genau so viele oder weniger Potenzen der Impulse wie in den Ausdrücken mit kleinerer Ordnung auftreten. Der Grad der Divergenz eines Integrales über einen Impuls ![]()
in einem Feynman-Diagramm kann nun direkt abgelesen werden.
Obwohl allzu technische Beiträge in diesem Artikel vermieden werden sollen, muß der Begriff des irreduziblen Feynman-Diagrammes eingeführt werden. Dabei handelt es sich um ein Diagramm, das nicht durch das Zerschneiden genau eines Propagators in voneinander unabhängige Teile separiert werden kann. Alle Feynman-Diagramme können auf einfache Weise in Produkte aus den irreduziblen Darstellungen zerlegt werden. Nur die irreduziblen Darstellungen, die zur Energie des Vakuums beitragen, besitzen einen Grad der Divergenz gleich der Raum-Zeit-Dimension ![]()
; alle anderen irreduziblen Diagramme sind weniger divergent. Man erkennt, daß nur diejenigen irreduziblen Diagramme, die zur Renormierung der Kopplungsparameter mit nicht-negativer Dimension beitragen, divergent sein müssen (abgesehen von den divergenten Sub-Diagrammen, die getrennt betrachtet werden müssen). Damit läßt sich die Bedingung zur Renormierung genauer formulieren: alle Wechselwirkungsterme, die konsistent mit einer gegebenen Symmetrie sind und durch einen Störungsparameter mit nicht-negativer Dimension beschrieben werden, müssen vorhanden sein. In diesem Fall sind die einzigen divergenten Integrale diejenigen, die Renormierungen der gegebenen Wechselwirkungsparameter entsprechen.
5 Regularisierung
Wir sind nun vorbereitet, eine strenge Strategie zur Definition einer sinnvollen Theorie entwerfen zu können. Dazu müssen wir zunächst die Theorie regulär machen, d.h. einige Abschneidebedingungen (cut-off) einführen, um alle Integrale endlich oder zumindest konvergent zu machen. Aus diesem Grund werden leichte Modifikationen der Theorie auf einer Abstandsskala eingeführt, die so klein ist, daß sie die zu beschreibenden Phänomene nicht direkt beeinflussen. Das einfachste Beispiel einer solcher Modifikation oder Regularisierung ist das Ersetzen des kontinuierlichen Raumes durch ein sehr feines Gitter (Lattice). Dieses sorgt automatisch dafür, daß alle Raumkomponenten des Impulses ![]()
auf den Bereich ![]()
beschränkt sind, wobei ![]()
eine große Zahl und ![]()
der Abstand zwischen den Gitterpunkten ist. Natürlich sind in einer solchen Theorie alle Integral(wert)e endlich. Da die Zeit weiterhin kontinuierlich ist, stellt sich zwar nicht das Problem mit der Unitarität, aber die Lorentz-Invarianz und sogar die Rotationsinvarianz gehen offensichtlich verloren.
Es ist nicht schwer zu erkennen, daß in diesem Ansatz ein kontinuierlicher Grenzwert existiert, außer in den Fällen, in denen das Integral divergiert. Dies tritt aber ja nur dann auf, wenn wir – wie bereits erwähnt – eine frei wählbare physikalische Konstante zur Hand haben und diesen Parameter so definieren bzw. renormieren können, daß er die Unendlichkeit neutralisiert. Wenn also die ›nackten‹ Konstanten für ![]()
einigen definierten Regeln folgend gegen Unendlich gehen, kann die Existenz eines kontinuierlichen Grenzwertes angenommen werden. Woran erkennt man aber in diesem Fall, daß die Lorentz-Invarianz in einem solchen Grenzwert wieder hergestellt wird? Gleichzeitig ist es nicht einfach, die Eichinvarianz auf einem so gewählten Gitter intakt zu halten.
Zu diesem Zweck wurden geschicktere Regularisierungen eingeführt, deren physikalische Interpretation ein wenig komplizierter ist. Die Pauli-Villars-Regularisierung ersetzt den Propagator ![]()
durch einen konvergenteren Propagator

wobei ![]()
wiederum eine große Zahl ist. Da
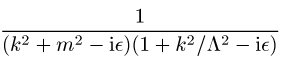

beschreibt dieser Propagator eine Theorie, in der ein zusätzliches Teilchen mit der Masse ![]()
eingeführt wird. Da dessen Propagator ein negatives Vorzeichen trägt, handelt es sich um kein gewöhnliches Teilchen. Das negative Vorzeichen deutet an, daß die Wahrscheinlichkeit, ein solches Teilchen in einem Streuprozeß zu erzeugen, negativ ist – eine physikalische Unsinnigkeit. Die Unitarität ist erhalten, aber nur in den Kanälen, in denen die Energie nicht ausreicht, schwere Teilchen zu erzeugen. Sind einige Integrale immer noch divergent, so muß die Prozedur wiederholt werden, und schon wenige Anwendungen sollten dafür sorgen, daß alle Integrale konvergieren.
Es ist wichtig zu wissen, daß die Äquivalenz zwischen dem Gitterregulator und dem Pauli-Villars-Regulator gezeigt werden kann, d.h. im Grenzwert ![]()
und ![]()
sind die durch beide Schemata produzierten Amplituden identisch, unter der Voraussetzung, daß die frei wählbaren Naturkonstanten mit Hilfe einiger Regeln aneinander angepaßt werden. Dies ist eine Eigenschaft, die alle ›guten‹ Regulatoren gemeinsam haben.
Die Pauli-Villars-Regularisierung besitzt zwar den Vorteil der Lorentz- und Rotationsinvarianz, aber damit ist das Problem noch nicht gelöst. Es existiert offensichtlich keine eichinvariante Lagrange-Dichte, die Propagatoren für die Vektorfelder erzeugt, welche das gleiche Konvergenzverhalten wie in Gl. (8) beschrieben besitzen. Ohne Eichinvarianz ist es allerdings schwer zu zeigen, ob die Slawnow-Taylor-Identitäten erfüllt werden können. Aus diesem Grund wurde ein dritter Regulator eingeführt, nämlich die sogenannte dimensionale Regularisierung.
Die dimensionale Regularisierung wird in zwei Schritten durchgeführt. Zunächst wird eine Definition dafür angegeben, was es bedeutet, wenn eine Theorie nicht in ![]()
(oder einer anderen ganzen Zahl), sondern in ![]()
Dimensionen zu beschreiben ist, wobei ![]()
eine kleine, aber nicht verschwindende Zahl ist. Dieser Schritt ist bemerkenswert einfach, da die meisten Integrationen in den Feynman-Diagrammen in sehr einfacher Art von der Raum-Zeit-Dimension abhängen und damit eine unkomplizierte Verallgemeinerung gestatten. In fast allen Fällen benötigt man lediglich das Integral über einen sphärischen Raum:

wobei für ![]()
jede (reelle oder komplexe) Zahl gewählt werden kann. ![]()
ist die Eulersche Gammafunktion (![]()
-Funktion). Zu beachten ist, daß die Lorentz-Indizes ![]()
von 1 bis ![]()
laufen und auch die Algebra der Dirac-Matrizen ![]()
von ![]()
abhängt.
Ist ![]()
nun keine ganze oder einfach rationale Zahl, so kann jedes divergente Integral relativ einfach durch einen endlichen Ausdruck ersetzt werden. Man kann zeigen, daß alle in den Feynman-Diagrammen auftretenden Integrationen in Teile separiert werden können, die für bestimmte (komplexe) Werte von ![]()
konvergieren. Diese können dann für alle ![]()
durch analytische Fortsetzung definiert werden. Nur diejenigen Integrale, die für bestimmte Integralwerte von ![]()
logarithmisch divergieren, besitzen in diesen Werten eine Singularität. Für ![]()
produzieren die Feynman-Amplituden Werte, die für ![]()
mit der inversen Potenz von ![]()
divergieren. Weil die ursprünglichen Integrale auch quadratische und andere Divergenzen besitzen, führt diese Definition eines endlichen Teils tatsächlich schon zu einer Renormierung der Kopplungsparameter, aber dies ist von geringer Bedeutung.
Es kann also gezeigt werden, daß die dimensional regularisierte Theorie im obigen Sinn äquivalent zu der Pauli-Villars- und der Gitter-regularisierten ist. Jetzt haben wir allerdings einen wichtigen Bonus erhalten: die dimensionale Regularisierung ist eichinvariant. Dieser Aspekt ist von großer Wichtigkeit für den nächsten Schritt.
6 Renormierung
Viele der nach einer der oben beschriebenen Vorschriften berechneten Amplituden divergieren weiterhin, wenn der Regularisierungsparameter ![]()
, ![]()
oder ![]()
gegen Null geht. Aus diesem Grund werden die frei wählbaren Parameter der Theorie durch ›nackte‹ Parameter ersetzt. In einer dimensional regularisierten Theorie schreibt man z.B.

wobei die renormierte Kopplung ![]()
konstant und endlich für alle Ordnungen ist. In einer renormierbaren Theorie können die Koeffizienten dieser Reihe so angepaßt werden, daß alle zu berechnenden Streuamplituden bis hin zu einigen Größenordnungen des (kleinen) Parameters ![]()
endlich und wohl definiert sind. Im allgemeinen Fall existieren verschiedene Kopplungsparameter, die alle in der Entwicklung auftauchen können.
Eine Komplikation tritt auf, wenn auch die off-shell-Amplituden endlich sein sollen. Sie entsprechen den Erwartungswerten von (Produkten von) Feldwerten ![]()
oder ![]()
in einigen S-Matrixelementen. Diese Felder, die nicht direkt beobachtbar sind, stellen Hilfsgrößen dar, die nützlich bei der Analyse einer Berechnung oder der Überprüfung der Slawnow-Taylor-Identitäten sind. Folglich können diese Ausdrücke immer noch Unendlichkeiten enthalten, die jedoch durch die Renormierung der Felder selbst eliminiert werden können. Die Tatsache, daß diese Feldrenormierungen explizit von der gewählten eichfixierenden Prozedur abhängen können, macht die Überprüfung der Eichinvarianz höchst heikel. Dies ist auch der Grund, warum der Autor dieses Artikels diese Identitäten ursprünglich nur für die physikalisch relevanten Amplituden, d.h. die on-shell-Amplituden, benutzt hat.
Es gibt einen wichtigen Fall, in dem die Renormierungsprozedur nicht angewendet werden kann: wenn die Theorie eine sogenannte Eichanomalie besitzt. Dieser Fall tritt z.B. dann auf, wenn Fermionen durch einen der Weyl-Projektionsoperatoren ![]()
chiral an ein Eichfeld gekoppelt sind. Da der Massenterm der Fermionen die Chiralität umschaltet, verletzt die Pauli-Villars- ebenso wie die Gitter-Regularisierung die Eichinvarianz. Auch die dimensionale Regularisierung wird komplizierter, wenn ![]()
ins Spiel kommt. Man hat herausgefunden, daß die Theorien mit Anomalie grundsätzlich inkonsistent sind, es sei denn die Eichanomalien verschwinden auf Einschleifenniveau (one-loop level). Dies steht in enger Beziehung zum Verhalten der Instantonen in der Theorie: Instantonen erzeugen einen Wechsel der Chiralität und verletzen somit bestimmte Symmetrien; sie sollten aus diesem Grund nicht an das Eichfeld koppeln. Im Standardmodell heben sich die Anomalien wie gewünscht weg. Eine notwendige Bedingung dafür ist, daß die Anzahl der Lepton- gleich der Anzahl der Quarkgenerationen ist (in unserer Welt sind beide gleich Drei).
Das Verschwinden der Anomalien auf one-loop-Level reicht aus, um ihre Auslöschung in allen Ordnungen beweisen zu können (eine von B. Lee und A. Slawnow unabhängig voneinander entdeckte eichinvariante Regularisierung löst sogar bei Anwesenheit des Termes ![]()
diese Aufgabe für höhere Ordnungen).
7 Die Renormierungsgruppe
Alle Regularisierungen haben gemeinsam, daß sie eine neue Skalenabhängigkeit in die Theorie einführen, auch dann, wenn die ursprüngliche Theorie skalenunabhängig war. Theorien wie die Quantenchromodynamik oder die Quantenelektrodynamik bei Energien wesentlich größer als ![]()
enthalten nur dimensionslose Parameter, aber die Regularisierung verursacht einen Zusammenbruch der Skalenunabhängigkeit. Die sogenannte Callan-Symanzik-Gleichung (Renormierungsgruppengleichung) beschreibt die neue Skalenabhängigkeit der Amplituden in einer solchen Theorie durch

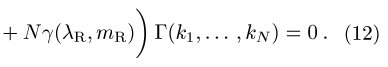
In dieser Gleichung beschreibt ![]()
die Energieskala, auf der die Renormierung definiert ist, ![]()
ist eine ![]()
-Teilchenamplitude, die sowohl von ![]()
als auch von ![]()
abhängt. Die Terme ![]()
, ![]()
und ![]()
sind die zu berechnenden Koeffizienten, die zeigen, wie die renormierten Massen ![]()
und Kopplungen ![]()
mit der Variation von ![]()
skalieren. (In den Originalarbeiten von Callan und Symanzik hat die obige Gleichung eine etwas andere Form.) Der entscheidende Ausdruck ist hier der ![]()
-Term. In allen älteren Theorien, d.h. den nicht eichinvarianten und der QED, ist ![]()
immer positiv, und dies wurde von Coleman und Gross allgemein bestätigt. Es war wie ein Schock, als man entdeckte, daß die nichtabelschen Eichtheorien einen negativen ![]()
-Koeffizienten besitzen können. Für die kleinste nicht-triviale Störungsordnung gilt
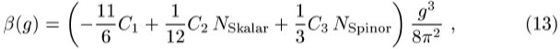
wobei ![]()
der sogenannte Casimir-Koeffizient der Eichgruppe, ![]()
die Anzahl der skalaren Teilchen in der einfachen Darstellung und ![]()
die Anzahl der (nicht-chiralen) elementaren Spinoren ist. Für die Farb-Eichgruppe SU(3) folgt ![]()
und ![]()
. Aus diesem Grund kann diese Theorie bis zu 16 Quark-Flavors enthalten, bevor ![]()
sein Vorzeichen ändert. Das negative Vorzeichen von ![]()
impliziert, daß die effektive Kopplung zu hohen Energien hin anwächst und somit die QCD bei hohen Energien störungstheoretisch behandelt werden kann (asymptotische Freiheit). Im Infraroten explodiert die Kopplungskonstante; dies bedeutet, daß sehr starke Kräfte entstehen. Dieser Aspekt kann erklären, warum Quarks permanent miteinander verbunden werden können (dieses Confinement-Phänomen kann aber auch auf viel bessere Weise verstanden werden).
In der allgemeinsten renormierbaren Quantenfeldtheorie mit vier Raumzeit-Dimension gibt es Skalarfelder (zur Beschreibung von Spin 0-Teilchen), Dirac-Felder (Spin 1 / 2-Teilchen) und Eichfelder (Spin 1-Teilchen). In diesem allgemeinsten Fall kann eine Mastergleichung für alle ![]()
-Koeffizienten aufgestellt und untersucht werden. Unter der Annahme der Anwesenheit von Eich- und Dirac-Feldern stellt sich heraus, daß die Skalarfelder nicht, wie teilweise angenommen, die asymptotische Freiheit unterdrücken. Die gegenwärtige Version des Standardmodelles ist nicht asymptotisch frei, da es ein ![]()
-Eichfeld enthält. Dies stellt aber kein Problem dar, da bei den höchsten Energien, bei denen dieses Modell glaubwürdig sein sollte (der Planck-Skala), die laufende ![]()
-Kopplungskonstante klein ist.
In der Festkörperphysik spielt die Renormierungsgruppe eine vergleichbar wichtige Rolle. Hier stellt man zunächst die Gleichungen der Theorie für das Molekülniveau auf und berücksichtigt dann die Effekte der Skalierung hin zu größeren Raum- und Zeitskalen. In diesem Fall kann eine Theorie selbst-ähnlich (self-similar) werden, aber da die relevante Zahl der Dimensionen ![]()
ist, wächst die effektive Kopplungsstärke beim Übergang zu größeren Skalen stark an. Dieser Schritt wurde von K. Wilson und M.E. Fischer gegangen, die verschiedene Prozeduren entwickelten, um die Freiheitsgrade kleiner Abstände auszuintegrieren, um so eine Theorie auf sich selbst bei höheren Skalen abzubilden. Auf diese Weise können die kritischen Koeffizienten eines statistischen Systems bestimmt werden. Da die Gleichungen aber nur integriert werden können, wenn man von kleinen zu großen Skalen übergeht, aber nicht umgekehrt, handelt es sich bei dieser Renormierungsgruppe lediglich um eine Halbgruppe.
8 Neue Entwicklungen
Zahlreiche Aspekte der Renormierung werden auch heutzutage weiterhin untersucht. Eine wichtige Eigenschaft wurde für supersymmetrische Eichtheorien gefunden. Diese Theorien tendieren aufgrund ihrer enorm vergrößerten Symmetrie dazu, grundsätzlich weniger Divergenzen zu besitzen. In der ![]()
Super-Yang-Mills-Theorie, einer Theorie mit vier Spinoren und sechs Skalaren in der adjungierten Darstellung (für die ![]()
gilt), konvergieren alle Schleifenintegrale. Tatsächlich liest man an Gl. (13) für diese Theorie ![]()
ab. Sie ist nicht nur skalierungsinvariant, sondern auch invariant unter allen konformen Raumzeit-Transformationen.
Die Renormierung der Quantengravitation wurde gründlich untersucht, aber da Newtons Konstante ![]()
, die als Störungsparameter benutzt wird, die Dimension -2 hat, ist diese Theorie nicht renormierbar. Für die aufeinanderfolgenden Ordnungen in der störungstheoretischen Entwicklung müssen der Lagrange-Dichte mehr und mehr neue Counterterme zur Renormierung hinzugefügt werden. In manchen Fällen wird die Anzahl dieser unerwünschten Terme durch die Symmetrie eingeschränkt. Werden keine Materiefelder eingeführt, so bleibt die reine Gravitation renormierbar auf Einschleifenniveau, einfach aus dem Grund, weil keine invariante Kopplung der entsprechenden Dimension existiert. Supergravitations-Theorien werden noch weiter durch die Supersymmetrie eingeschränkt, aber bei ihnen treten unvermeidliche Divergenzen bei höheren Störungsordnungen auf. Moderne Theorien benutzen zumeist eine größere Raumzeit-Dimension als Ausgangspunkt, wobei die zusätzlichen Dimensionen kompaktifiziert sind (Kompaktifizierung), aber auch das zerstört die Renormierbarkeit. Die Superstring-Theorie (String-Theorie) ist ebenfalls in einem 10-dimensionalen Raum definiert, aber deren Symmetrien sind so gewaltig, daß alle Schleifenintegrationen konvergieren und keine Renormierung nötig ist.
Sowohl die Theorien zur Beschreibung von Elementarteilchen als auch die zur Beschreibung der kondensierten Materie besitzen heute eine Schichtenstruktur: für verschiedene typische Abstände und Zeitbereiche werden verschiedene Modelle zu deren Beschreibung herangezogen, und bei einer kontinuierlichen Änderung der Skala variieren die relevanten Kopplungsparameter entsprechend. In diesem Fall spricht man von einer ›laufenden› Kopplungsstärke (running coupling). Wird der Kopplungsparameter für eine bestimmte Skala sehr groß, wird die störungstheoretische Behandlung ungeeignet und muß durch eine effektivere, alternative Beschreibung mit kleineren Störungskopplungen ersetzt werden. Die Quantenchromodynamik ist für alle Energiebereiche von 1 GeV bis hin zu einigen tausend TeV geeignet, unterhalb von 1 GeV müssen allerdings Hadronen, wie z.B. Pion, Proton und Neutron, betrachtet werden. Bei kleinen Energien sind deren effektiven Kopplungen sehr schwach, und es bieten sich zur effektiven Beschreibung einfache Hadronen-Modelle an. Bei noch kleineren Energien, d.h. größeren Abständen, können nicht-relativistische Modelle herangezogen werden, die z.B. Atomkerne beschreiben.
Dieser Artikel konnte hoffentlich einige der grundsätzlichen Geheimnisse lüften, die mit der Renormierung verbunden sind.
Literatur:
Geschichte der Renormierung:
A. Pais, Inward bound: of matter and forces in the physical world, Oxford University Press 1986.
R.P. Crease und C.C. Mann, The Second Creation: makers of the revolution in twentieth-century physics, New York, Macmillan, 1986.
G. 't Hooft, In search of the ultimate building blocks, Cambridge University Press 1997.
Renormierung in Eichtheorien:
G. 't Hooft und M. Veltman, DIAGRAMMAR, CERN Report 73/9 (1973), Neudruck in: D. Speiser et al (Hrsg.), Particle Interactions at Very High Energies, Nato Adv. Study Inst. Series, Sect. B, Vol. 4b (1973), S. 177; und: G. 't Hooft, Under the Spell of the Gauge Principle, Adv. Series in Math. Phys. Vol 19, World Scientific, Singapore, 1994.
Über Quantenfeldtheorie und Renormierung:
L.H. Ryder, Quantum Field Theory, Cambridge University Press, 1985, 1996.
C. Itzykson und J.-B. Zuber, Quantum Field Theory, Mc.Graw-Hill, New York 1980.
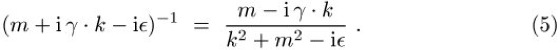






Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.