Eigentlich ist Ulrich Mikloweit Chemiker; sein Geld verdient er als Umwelt- und Abfallbeauftragter des Klinikums der Universität Essen. Aber auch Chemiker müssen sich gelegentlich mit Geometrie befassen, und zwar wenn es um Kristallstrukturen geht. In diesem Zusammenhang bekam der Chemiestudent Ulrich Mikloweit 1974 die Aufgabe, in Gedanken alle Flächendiagonalen in einem Würfel zu ziehen und zu ermitteln, zu welchen Körpern sich diese insgesamt zwölf Strecken fügen. Die Antwort: Es handelt sich um zwei regelmäßige Tetraeder, die einander durchdringen.

Bereits Johannes Kepler (1571-1630) beschrieb diesen Körper und gab ihm seinen heute gebräuchlichen Namen "Stella octangula" (achtspitziger Stern). Er ist zugleich das einfachste Beispiel für ein äußerst fruchtbares Konzept: die Dualität. Im Prinzip macht man aus einem Polyeder (einem von ebenen Flächen begrenzten Körper) ein anderes, indem man alle Flächen durch Ecken ersetzt und umgekehrt. Wenn bei dem ursprünglichen Polyeder zwei Flächen eine gemeinsame Kante haben, dann sind bei dem neuen (dem "dualen") Polyeder die zugehörigen Ecken durch eine Kante verbunden und umgekehrt.

Diese vorläufige Beschreibung sagt noch nichts über die Größenverhältnisse; bei einigermaßen regelmäßigen Körpern ist es jedoch möglich und sinnvoll, das duale Polyeder so zu bemessen, dass die Kanten von altem und neuem Polyeder sich genau in der Mitte rechtwinklig schneiden. Das ist insbesondere bei der Stella octangula der Fall. Das Tetraeder ist dual zu sich selbst, während die übrigen vier platonischen Körper paarweise – Würfel zu Oktaeder und Dodekaeder zu Ikosaeder – zueinander dual sind.

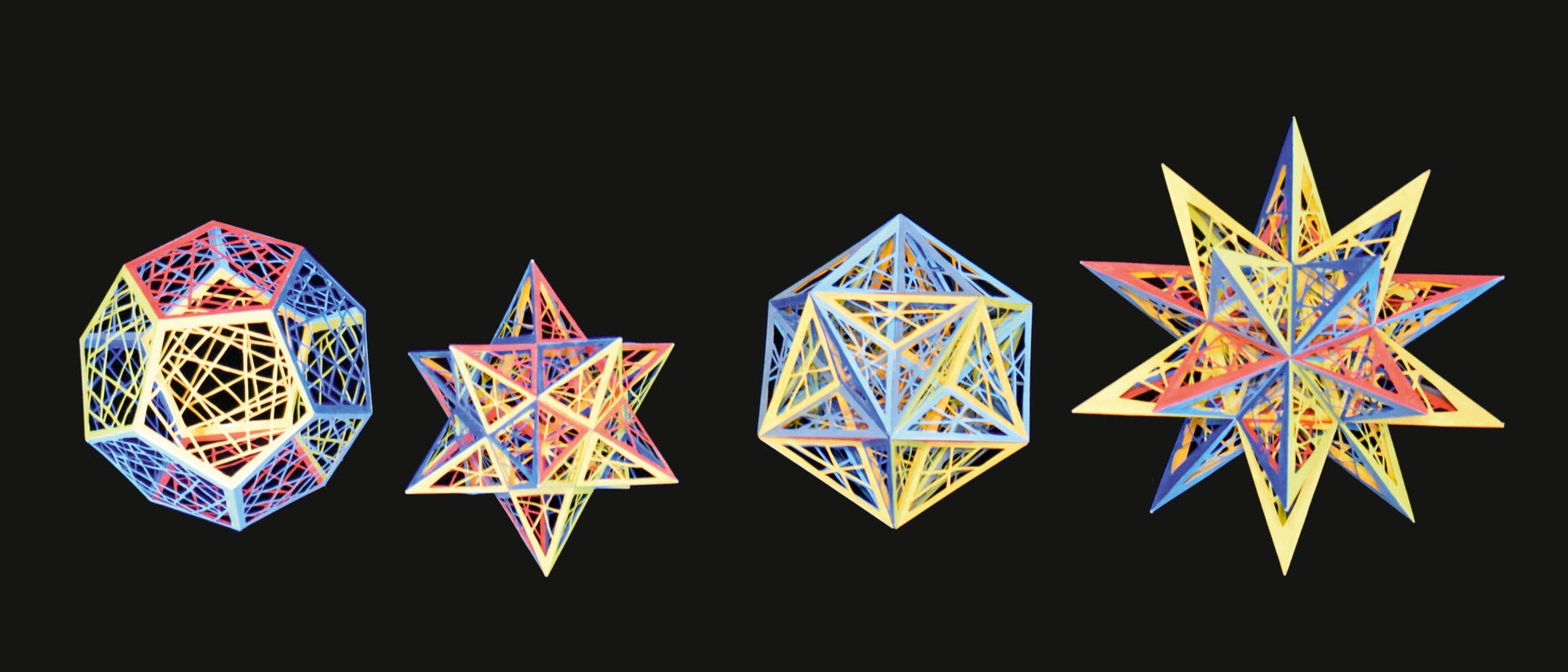
Auf den ersten Blick sieht man bei der Stella octangula jedoch nicht die vier Dreiecke, aus denen jedes Tetraeder besteht, sondern viele kleine. Der innere Teil jedes Dreiecks ist, da vom jeweils anderen Körper verdeckt, dem Blick entzogen. Das missfiel dem Studenten, und er sann auf Abhilfe: Man gehe zu durchbrochenen Flächen über, die wie Spitzendeckchen oder Gittertore den Durchblick auf das Darunterliegende zulassen ...