Es gibt eine ganze Reihe von Problemen, die herkömmliche Computer schnell an den Rand ihrer Leistungsfähigkeit bringen. Das Problem des Handlungsreisenden, der die kürzeste Reiseroute auf seinem Weg durch viele Städte bestimmen möchte, gehört dazu. Ebenso die Aufgabe, eine Landkarte mit möglichst wenig Farben so einzufärben, dass benachbarte Länder immer in unterschiedlichen Farben dargestellt sind. Solange der Handlungsreisende nur wenige Städte bereist oder nur wenige Länder auf der Landkarte verzeichnet sind, lässt sich die beste Lösung auf einem Computer schnell durch Ausprobieren aller möglichen Kombinationen finden. Doch die Anzahl dieser Kombinationen steigt rasant an, wenn viele Städte oder Länder berücksichtigt werden müssen. Zu viel für herkömmliche Rechner, ein Quantencomputer muss her. Dachte man jedenfalls bisher.

Die wirtschaftliche Bedeutung solcher kombinatorischen Probleme ist immens. Das Problem des Handlungsreisenden ist nicht nur ein einfaches akademisches Beispiel. So können etwa Speditionen, Reedereien und Fluggesellschaften sehr viel Treibstoff und Geld sparen, wenn sie ihre Fahrten und Leerfahrten möglichst geschickt verteilen. Sie gehören jedoch zu einer Klasse von Aufgaben, die man "NP-schwer" nennt: Herkömmliche Computer benötigen mit ansteigender Komplexität überproportional viel Zeit, um diese Probleme zu bewältigen.

Oft lassen sich auch mit viel Geschick nur gute Näherungslösungen statt der optimalen Antwort finden. Jetzt allerdings macht ein neuer Computertyp – halb Quantenmaschine, halb klassischer Computer – Fachleuten Hoffnung auf Fortschritte bei diesen kniffligen Problemen: Zwei kollaborierende Forscherteams von den NTT Labs in Japan und der Stanford University in den USA haben einen neuartigen Computertyp realisiert, der nicht auf der klassischen "Von-Neumann-Architektur" beruht, sondern auf dem so genannten "Ising-Modell".

Moderne Computer nutzen jene Arbeitsprinzipien, die der Mathematiker und Physiker John von Neumann im Jahr 1945 entwickelte. Zum Lösen bestimmter kombinatorischer Aufgaben eignet sich, zumindest in der Theorie, aber ein anderer Computertyp besser. Er beruht auf einem Modell des deutschen Physikers Ernst Ising, der mit ihm das Verhalten magnetischer Materialien analysieren wollte.

Das Ising-Modell

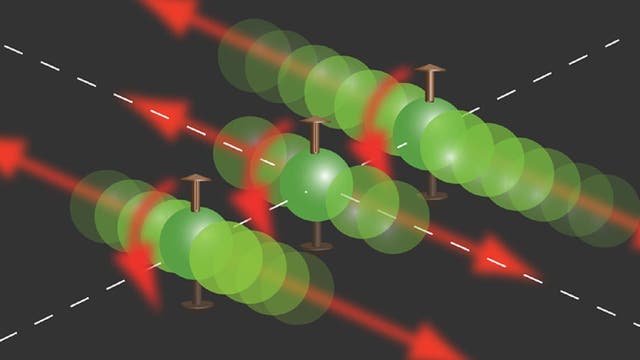
Beim Ising-Modell rechnet man mit einer Reihe Elementarmagnete ("Spins"), die sich wechselseitig beeinflussen können. Der Einfachheit halber nahm Ising an, diese Spins könnten immer nur mit ihren Nachbarn wechselwirken und sie könnten nur nach oben oder unten zeigen, was plus oder minus eins entspricht – oder in der binären Darstellung der Informatik als Bit einer "1" und einer "0".

Mit diesem Modell lassen sich, wenn man es in zwei oder drei Dimensionen betrachtet, einige magnetische Phänomene sehr gut beschreiben. Dafür hatte es Ising 1924 entworfen. Es hat sich deshalb in der statistischen Physik – bei der es um die Untersuchung des Verhaltens vieler miteinander gekoppelter Teilchen geht – als Standard-Arbeitsmittel etabliert.

Ein wichtiger Schritt zur Nutzung des Ising-Computers war, dass Mathematiker dieses Modell verallgemeinern konnten: Im generalisierten Ising-Modell beeinflussen sich nicht nur benachbarte, sondern auch weit voneinander entfernt liegende Spins wechselseitig. Auf diesem Weg erhält man ein System, das wie geschaffen ist für komplexe kombinatorische Probleme. Und das sind genau die, mit denen herkömmliche Computer Probleme haben. Der Handlungsreisende und die gefärbte Karte gehören dazu. Einige Forschergruppen weltweit hatten deshalb schon versucht, unter anderem mit supraleitenden Elementen solche "Ising-Architekturen" zu verwirklichen. Allerdings stießen sie dabei auf das gleiche Problem, das die Mathematik mit solchen Systemen hat: Sie werden unverhältnismäßig schnell komplex.

Wenn etwa 1000 Spins sich gegenseitig beliebig beeinflussen können, entspricht das einer Million wechselseitigen Abhängigkeiten. Ein System wie das ursprüngliche Ising-Modell, das immer nur zwischen benachbarten Spins Datenaustausch erlaubt, würde dann eine Million Komponenten benötigen! Und bei schwierigeren Problemen steigt diese Anzahl weiter quadratisch an.

Ein realer Ising-Computer muss also die Verknüpfung weit auseinanderliegender Spins physisch umsetzen, um nicht dem quadratischen Wachstum zum Opfer zu fallen. Dieses Problem, an dem sich Fachleute lange die Zähne ausgebissen haben, scheint nun durch einen kleinen Trick gelöst zu sein. Ein klassischer Computer berechnet die Zustandsänderungen, die sich von jedem Spin durchs System ausbreiten. Die beiden Forscherteams aus Japan und den USA entwickelten ein System mit beliebigen Wechselwirkungen zwischen allen Komponenten. "Mit unserem Design können wir ein 1000-Spin-Problem mit einer Maschine lösen, die tatsächlich nur 1000 physische Spins besitzt", sagt Peter McMahon von der Stanford University.

Von der Theorie zur Praxis

Das Besondere am System der beiden Gruppen: Sie nutzten einen gemischten Aufbau aus optischen Bauteilen und schneller Auswertungselektronik. In einem langen Glasfaserkabel von einigen hundert Metern Länge brachten sie so genannte optisch parametrische Oszillatoren an – Bauteile, die je nach ihrer Voreinstellung auf einen polarisierten Laserpuls mit einer positiven oder negativen Zustandsänderung reagieren.

Gleichzeitig gaben die Oszillatoren bei jedem Durchlauf ein Signal ab, das die Forscher mit einer sehr schnellen elektronischen Schaltung auslasen. Dadurch konnten sie deren Einstellungen über einen Algorithmus, der das jeweilige Problem darstellt, für den nächsten Durchlauf passend ändern. Auf diese Weise kam das System mit jedem Durchlauf des Laserpulses der Lösung des Problems immer näher. Meist schon nach wenigen Dutzend Durchläufen ergab sich so eine zumindest sehr gute Annäherung an die optimale Lösung. Warum sich dieses System so verhält, ist allerdings rätselhaft.

Die Aufbauten der beiden Gruppen unterscheiden sich nur durch ihre Größe: Die Gruppe in Japan stattete ein längeres Kabel mit 2000 Oszillatoren aus, die Gruppe in Stanford nutzte nur 100. Gemeinsam ist beiden Gruppen auch, dass die bisher mit der Maschine gelösten Probleme noch keinem Handlungsreisenden oder Kartenzeichner helfen werden: Die untersuchten Probleme waren sehr abstrakte mathematische Aufgaben aus der Graphentheorie. Für realistischere Aufgaben müssen die Forscher die Maschine erst noch erweitern. "Wir wollen das Problem des Handlungsreisenden und das Einfärben von Landkarten in zwei Jahren ausprobieren", sagt Takahiro Inagaki von den NTT Labs.

Was auf den ersten Blick wie eine überraschende neue Technologie aussieht, muss den Test in der Praxis also erst noch bestehen. Die Forscher konnten zwar bereits zeigen, dass ihre Maschine spezielle kombinatorische Probleme ähnlich schnell oder sogar schneller löst als ein herkömmlicher Computer. Wie das allerdings bei sehr komplexen Problemen sein wird, wenn solche "Ising-Maschinen" wegen der zunehmenden Baugröße vielleicht mit Schwierigkeiten wie Rauschen und einer komplexeren Ansteuerung zu kämpfen haben werden, ist noch nicht ausgemacht. Die Forscher planen aber bereits, die Anzahl an Spins deutlich zu erhöhen, womit sie in einigen Jahren in die Nähe kommerzieller Anwendungen geraten dürften.