Apfelkuchen

Ariane hat zum Schulfest, das auf ihren eigenen Geburtstag fällt, ein quadratisches Blech voll Apfelkuchen mitgebracht und angekündigt: Der erste Gast bekommt 1/4, der zweite 1/16, der dritte 1/64 usw., also bekommt der Gast Nr. n (1/4)n vom Kuchen. Welchen Teil des Kuchens kann sie am Abend mit ihren Geschwistern zu Hause verspeisen, wenn unendlich viele Gäste zum Schulfest kommen und ihren Teil abholen?
Malen Sie Quadrate in ein großes Quadrat.
Jede (noch so große!) endliche Zahl von Gästen bekommt zusammen weniger als 1/3 des Kuchens, der Grenzwert für unendlich viele ist genau 1/3.
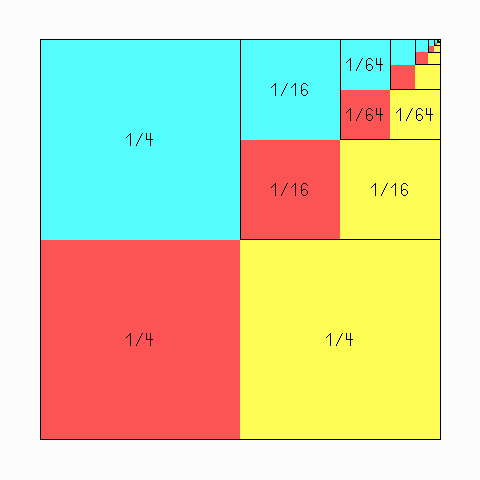
Das Quadrat wird durch die schwarzen Linien in Teile zerlegt, die jeweils aus drei gleichen Quadraten (je einem roten, einem blauen und einem gelben) bestehen. Es ist also 1/4 + 1/16 + 1/64 + usw. = 1/3. Im Dezimalsystem liest sich das so: 0,25 + 0,0625 + 0,015625 + ... = 0,33333333...
Im Binärsystem addieren wir entsprechend 0,01 + 0,0001 + 0,000001 + usw. = 0,0101010... und finden unser Bild wieder.
Man kann das Ganze natürlich auch als Spezialfall der geometrischen Reihe auffassen mit den Gliedern (1/4)n. Für n=0 bis Unendlich kommt dann 1/(1–(1/4)) = 4/3 heraus, und wenn man mit n=1 anfängt, 1/3.
Vergleichen Sie auch die Aufgabe zum Pflaumenkuchen, die auf dem gleichen Schulfest stattfindet und so ähnlich aussieht, wenigstens auf den ersten Blick (?).



Schreiben Sie uns!
Beitrag schreiben