Hemmes mathematische Rätsel: Crux Numerorum
Die britische Wochenzeitung »The Sunday Times« stellt ihren Lesern seit 1961 jeden Sonntag einen »Brain Teaser«. Das heutige Rätsel ist ein »Brain Teaser« aus den 1970er-Jahren.
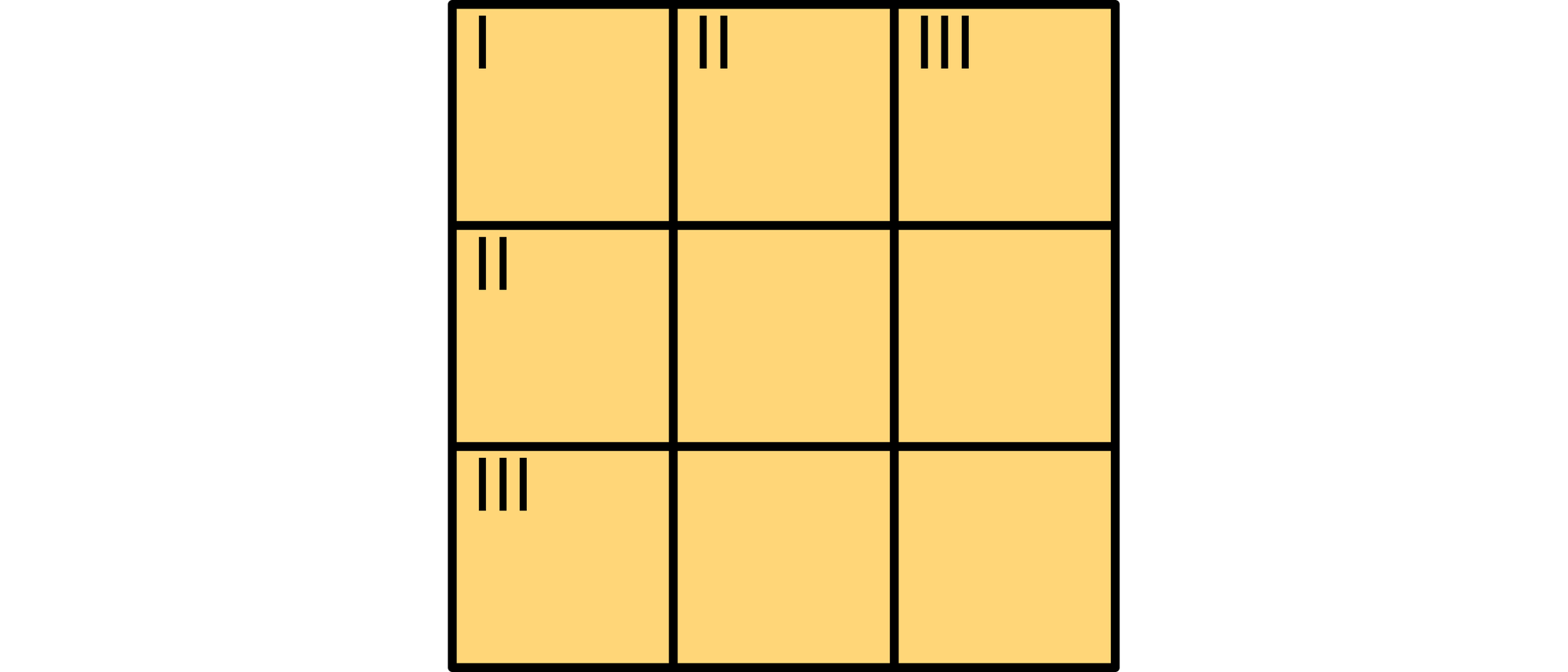
Professor Digby-Nite fand bei Ausgrabungen am Hadrianswall ein Tontäfelchen aus der Römerzeit in das ein Raster aus neun Quadraten eingeritzt worden war. Es war ein Crux numerorum, ein Kreuzzahlrätsel. Daneben standen einige Hinweise.
Waagerecht:
I Vielfaches von XXXVII
II Vielfaches von LXXIII
III Faktor von I senkrecht
Senkrecht:
I Quadratzahl
II Vielfaches von VII
III Calpurnias Alter
In die Felder dürfen keine arabischen Ziffern, sondern nur römische Zahlenzeichen gesetzt werden. Wie alt war Calpurnia?
Die kleinste dreistellige römische Zahl ist III = 3 und die größte MMM = 3000. Betrachten wir zunächst einmal II waagerecht. Es ist leicht, in diesem Zahlenbereich zu überprüfen, welche Vielfachen von LXXIII = 73 dreistellige römische Zahlen sind. Es gibt nur ein einziges, nämlich 7 · 73 = 511 = DXI. Folglich muss das mittlere Zeichen von I senkrecht ein D sein. In einer römischen Zahl kann vor einem D nur ein M oder ein C stehen. Die einzige Quadratzahl, die in römischer Schreibweise dreistellig ist und mit MD oder CD beginnt, ist MDC = 1600. Damit ist das erste Zeichen vom I waagerecht ein M.
Die einzige dreistellige römische Zahl, die mit M beginnt und ein Vielfaches von XXXVII = 37 ist, ist 30 · 37 = 1110 = MCX. Nun kann man auch II senkrecht leicht bestimmen, denn das einzige in römischer Schreibweise dreistellige Vielfache von VII = 7 ist 20 · 7 = 140 = CXL. Jetzt fehlt nur noch III waagerecht. Der einzige Teiler von 1600, der in römischer Schreibweise mit CL beginnt, ist 160 = CLX. Damit ist das Quadrat vollständig gefüllt. Calpurnia ist also XIX = 19 Jahre alt.







Schreiben Sie uns!
Beitrag schreiben