Hemmes mathematische Rätsel: Damesteinsprünge
Manchmal findet man Schätze der Unterhaltungsmathematik, wo man sie gar nicht vermutet. Von 1842 bis 1894 erschien in den USA eine monatliche Zeitschrift für Bauern mit dem Titel The American Agriculturist. Neben vielen Artikeln über die Landwirtschaft und Anzeigen über Saatgut, Pflüge und Eggen enthielt sie auch eine Kolumne mit mathematischen Denksportaufgaben. Im Juni 1867 wurde in ihr erstmals das Damesteinsprungproblem veröffentlicht.
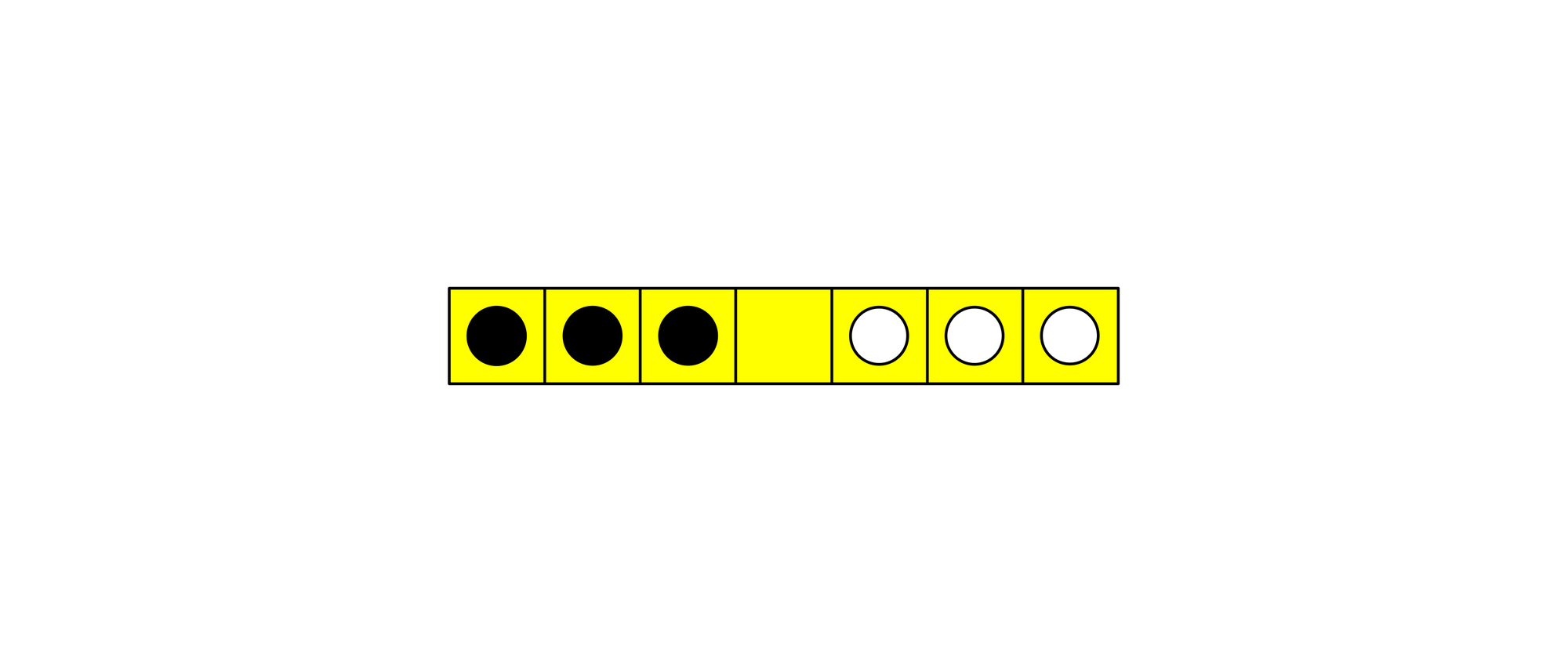
Auf einem Spielbrett, das nur einzige Reihe mit sieben Felder hat, liegen auf den ersten drei Feldern schwarze Damesteine und auf den letzten drei Feldern weiße Damesteine. Die schwarzen und weißen Steine sollen mit möglichst wenigen Zügen ihre Plätze tauschen. Dabei ist ein Zug das Verschieben eines Steins auf ein direkt benachbartes freies Feld oder das Springen mit einem Stein über einen einzelnen anderen Stein auf ein freies Feld. Außerdem dürfen die schwarzen Steine nur nach rechts und die weißen nur nach links gezogen werden. Wie viele Züge sind für den Tausch mindestens notwendig und welche sind es?
Durch fünfzehn Züge können die schwarzen und die weißen Damensteine ihre Plätze tauschen. Nummeriert man die Felder des Spielbretts von links nach rechts von 1 bis 7 durch, lauten die fünfzehn Züge:
- 3 → 4
- 5 → 3
- 6 → 5
- 4 → 6
- 2 → 4
- 1 → 2
- 3 → 1
- 5 → 3
- 7 → 5
- 6 → 7
- 4 → 6
- 2 → 4
- 3 → 2
- 5 → 3
- 4 → 5
Beweis der optimalen Lösung von Gudrun Schirmer
Die Grundschullehrerin Gudrun Schirmer aus Erlangen präsentiert einen Beweis, dass die hier vorgestellte Lösung auch wirklich die optimale ist:
Um an die neuen Plätze zu kommen, muss jeder Stein 4 Felder wandern. 6 mal 4 = 24 Schritte, die insgesamt zurückgelegt werden.
Diese Anzahl reduziert sich aber durch die Sprünge. Da jeder Stein alle andersfarbigen Steine überspringen muss, springt er 3 Mal. Jeder Sprung hilft beiden Farben, den jeweiligen Gegner zu überwinden und zählt deswegen doppelt.
Von den 24 Schritten muss man daher 18 Schritte abziehen, die durch die Sprünge überwunden werden, so dass bloß noch 6 übrig bleiben. Insgesamt benötigt man also mindestens 6 Schritte und 9 Sprünge, das heißt 15 Züge.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.