Ein Umkreis im Fünfeck
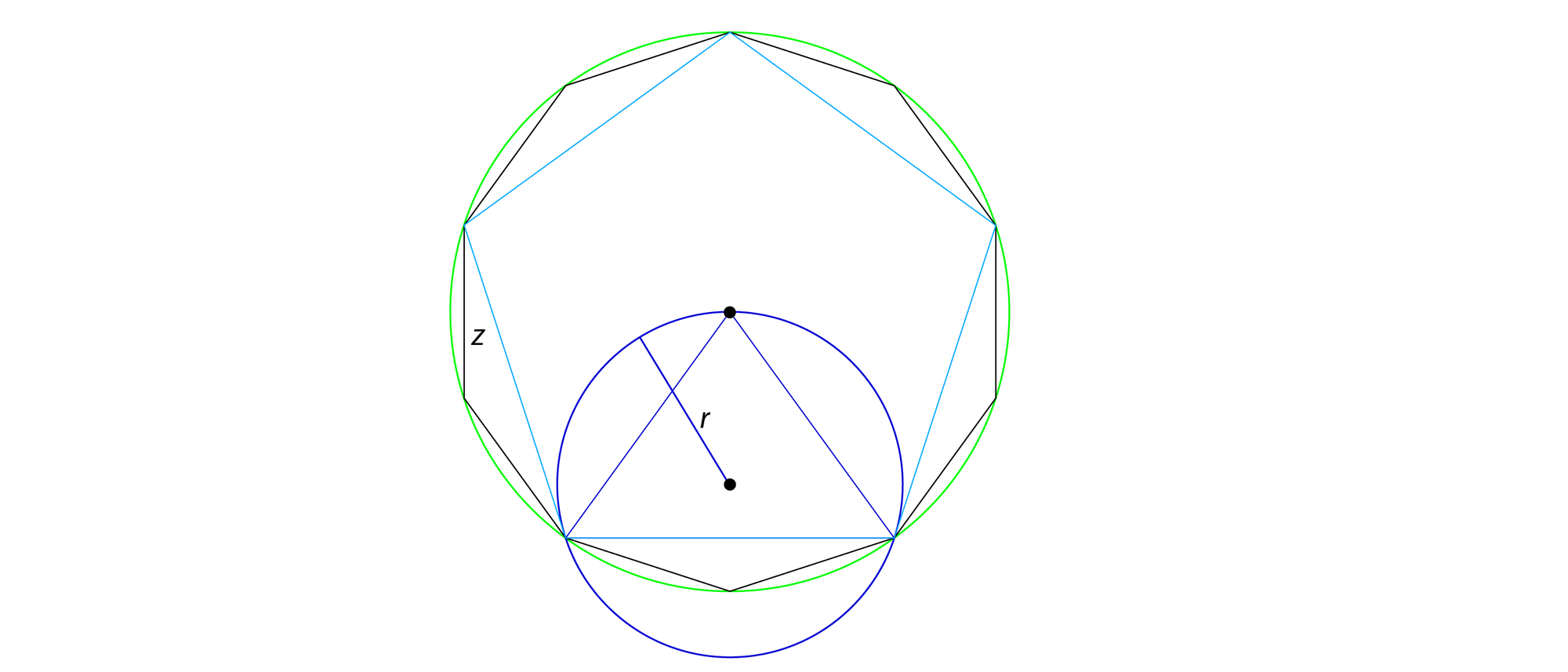
Zuerst bildet man den Umkreis eines Dreiecks, das sich aus zwei benachbarten Ecken eines regelmäßigen Fünfecks und dessen Mittelpunkt ergibt. Dann zeichnet man den Umkreis des Pentagons ein und ergänzt darin ein regelmäßiges Zehneck.
Warum sind der kleine Radius \(r\) vom Umkreis des Dreiecks und die Kante \(z\) des Zehnecks gleich lang?
Das rote und das blaue gleichschenklige Dreieck sind einander ähnlich, denn ihre Seiten sind paarweise parallel zueinander; also haben beide Dreiecke gleiche Winkel. Die zentrische Streckung, die aus dem roten Dreieck das blaue macht, bildet auch ihre Umkreise und deren Mittelpunkte aufeinander ab, ebenso die (grau gestrichelt eingezeichnete) Sehne \(s_1\) des Zehnecks auf ihre parallele Kollegin \(s_2\). Da \(s_2\) außerdem einer Zehnecksseite parallel ist und durch den Mittelpunkt des kleinen Umkreises verläuft, sind die zwei untersten Zehnecksseiten den (violett eingezeichneten) Radien des kleinen Umkreises nicht nur parallel, sondern aus Symmetriegründen auch gleich lang, was zu beweisen war.
Schreiben Sie uns!
Beitrag schreiben