Erweitertes Viereck
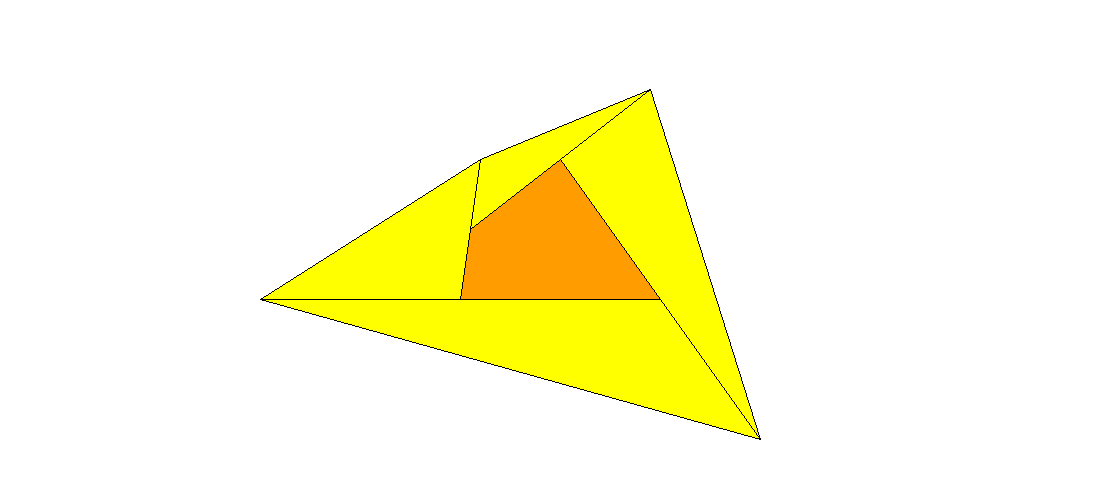
Das konvexe Viereck in der Mitte wird dadurch erweitert, dass man zyklisch jede Seite nach einer Richtung hin verdoppelt und damit die neuen Ecken bekommt. Um welchen Faktor vergrößert sich dabei die Fläche?
Ergänzen Sie die vier Dreiecke zu Parallelogrammen und suchen Sie darin Teile des ursprünglichen Vierecks.
Zunächst zerlegen Sie das ursprüngliche Viereck in zwei Dreiecke: ein grünes und ein dunkelblaues. Indem Sie dann zwei gegenüberliegende (ursprünglich gelbe) Dreiecke zu Parallelogrammen verdoppeln, können Sie darin die Anteile der Fläche des ursprünglichen Vierecks berechnen.
In den zwei Parallelogrammen taucht das Vierfache der ursprünglichen Vierecksfläche auf. Somit haben die zwei angefügten gelben Dreiecke die doppelte Fläche des ursprünglichen Vierecks.
Bei den anderen zwei Dreiecken kann man analog vorgehen: Man unterteilt das ursprünglich orangefarbene Viereck in zwei andere Dreiecke (rot und lila) und erweitert die anderen zwei Dreiecke zu Parallelogrammen, die man wiederum in kleinere Dreiecke unterteilt.
Auch in diesem Fall nehmen die zwei Parallelogramme das Vierfache der Fläche des ursprünglichen Vierecks ein.
Insgesamt kommt also durch die vier gelben Dreiecke das Vierfache der Fläche des ursprünglichen Vierecks hinzu.
Und wie ist es, wenn man die Seiten nicht um ihre eigene Länge verlängert, sondern um das \(x\)-Fache davon?
Die Parallelogramme und damit auch der ganze Zuwachs werden dann um den Faktor \(x\cdot \frac{1 + x}{2}\) größer. Für \(x = 2\) gibt das einen Zuwachs von 1 um 12 auf 13, für \(x = 0{,}5\) einen von 1 um 1,5 auf 2,5.
Wie steht es mit symmetrischen Spezialfällen (Raute, Rechteck und so weiter)?
Da die Operation zyklisch orientiert ist, wird 2- beziehungsweise 4-zählige Drehsymmetrie bewahrt, das heißt aus einem Parallelogramm (auch Raute oder Rechteck) wird wieder ein Parallelogramm (aber nicht unbedingt eine Raute oder ein Rechteck), und aus einem Quadrat wird immer ein Quadrat.
Schreiben Sie uns!
Beitrag schreiben