Stellen Sie sich Ihre Zahlen auf der Skala eines Rund-Rechenschiebers vor, der so aussieht:

Wenn man die Skala gleichmäßig unterteilt (rote Bezifferung), findet man 30% für die Anfangsziffer 1 und 4,5% für die 9.

Aber warum ist der (Rund-)Rechenschieber hier zuständig? Dahinter steckt das Benford-Gesetz.

Über diesen empirischen Zusammenhang findet man nur selten etwas, und dann erstaunlich unsicher formulierte Aussagen, so als sei das Ganze extrem rätselhaft.

Zunächst ist zu klären, warum wir keine Haus- oder Telefon-Nummern etc. nehmen: Wenn in einer Siedlung alle Straßen 100 Häuser haben, kommen nicht nur alle Nummern, sondern auch alle Anfangsziffern gleich oft vor. Wenn alle Straßen 70 Häuser haben, kommen die Ziffern 7, 8 und 9 seltener vor, und das Ganze hat nichts mit dem Zufall zu tun.

Nun nehmen wir die Körpergröße (also vertikale Länge) von erwachsenen Menschen: Sie liegen meistens zwischen 1 und 2 Meter, fangen also fast alle mit 1 an. Das ändert sich aber grundlegend, wenn wir sie in Fuß (etwa 0,3 m) angeben: Dann fangen die meisten mit 5 oder 6 an. Nehmen wir nun statt Menschen beliebige Tiere, so kommen Längen von Bruchteilen von Millimetern bis zu 30 m vor, etwa über 5 Zehnerpotenzen verteilt. Daran ändert sich auch nicht viel, wenn wir das in Fuß umrechnen.

Greifen wir uns nun die Tiere zwischen 1 und 1,1 Metern heraus, so sind es die gleichen wie zwischen 3,33 und 3,63 Fuß. Um die Argumentation übersichtlicher zu machen, denken wir uns als Längeneinheiten "halbe Zentimeter" und "Viertelzentimeter". Alles, was zwischen 3 und 4 cm ist, also bei Angabe in cm mit 3 anfängt, fängt bei Umrechnung in halbe cm mit 6 oder 7 an und bei Viertelzentimetern mit den Ziffernpaaren 12 bis 15, also mit 1.

Da es bei unseren Zahlen nicht darauf ankommt, ob sie Längen oder Massen oder Einwohnerzahlen usw. bezeichnen, kann es auch keine Rolle spielen, ob wir Meter, Fuß oder halbe Zentimeter als Einheiten nehmen. Wir brauchen also eine Bewertung der Intervalle, die sich beim Malnehmen aller Zahlen mit einem Faktor nicht ändert. Das Intervall von 1 bis 2 muss also so viele Beispiele haben wie das von 2 bis 4 oder das von 4 bis 8, das von 1 bis 3 so viele wie das von 3 bis 9.

Die derart konstruierte Skala ist gerade die logarithmische (ohne dass wir darüber hier mehr wissen müssten).

Das Benford-Gesetz liefert also im Dezimalsystem für die Anfangsziffern die folgende Verteilung:

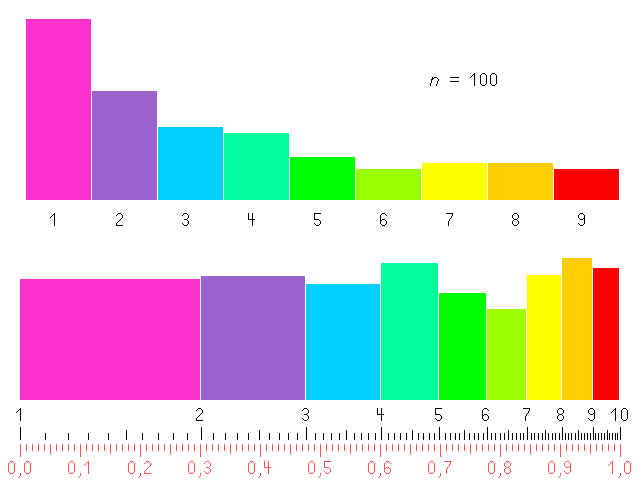
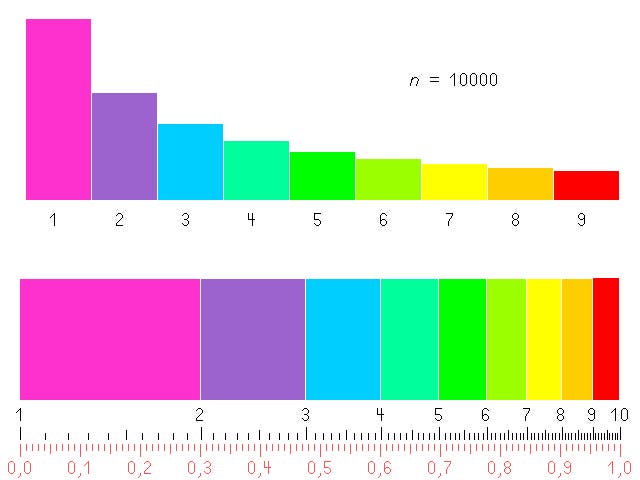
Die folgenden Grafiken sind so erzeugt worden: Die ersten 100 bzw. 10000 Potenzen von 1,5 (also 1, 1,5 , 2,25 usw.) wurden nach ihren Anfangsziffern einsortiert. Durch das Potenzieren wurden verschieden große Zahlen erzeugt, die keine Dezimalziffer bevorzugen (10 wäre nicht so gut gewesen).