Gutheil
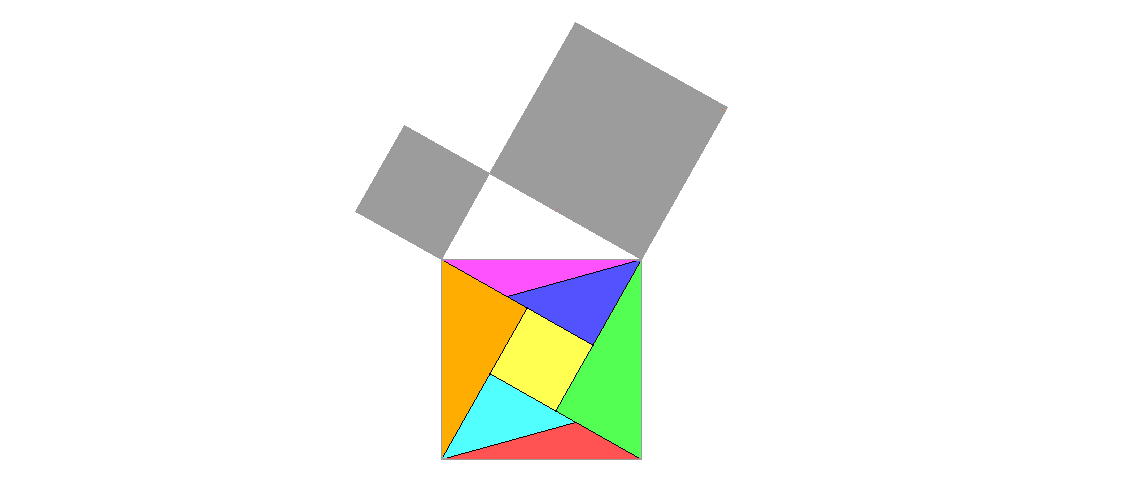
Der Puzzle-Beweis von Gutheil für den pythagoreischen Satz ist nicht besonders einfach, aber besonders symmetrisch.
Hier sehen Sie erst einmal nur das Hypotenusen-Quadrat zerlegt. Können Sie die Zerlegung in dieser Art weiterführen und so den Satz des Pythagoras beweisen?
Die Animation zeigt den Beweis nacheinander für verschiedene Dreiecke. Jedes Einzelbild des Videos ist also eine Beweisskizze:
Ich bin durch einen Vortrag von Heinz Klaus Strick aus Leverkusen auf diesen Beweis aufmerksam gemacht worden. Er zeigt allerdings – im Gegensatz zu anderen Pythagoras-Beweisen – nicht den Kathetensatz, und einige der immerhin sieben Polygone müssen gedreht oder sogar geklappt werden.
Über den Autor Benjir von Gutheil ist nicht viel ausfindig zu machen. Sicher scheint nur, dass er Oberlehrer in Nürnberg war und bereits am Beginn des Ersten Weltkriegs im Schützengraben in Frankreich gefallen ist.



Schreiben Sie uns!
Beitrag schreiben